File mat merupakan file hasil olah Matlab sebelumnya (image processing, jaringan syaraf tiruan, dan lain-lain). Biasanya hasil oleh ini disimpan dalam file dengan instruksi save <nama_file> dan diberikan ekstensi oleh matlan mat.
Pertama-tama persiapkan satu folder untuk program yang akan kita buat. File mat harus diletakkan pada folder kerja tersebut (pada matlab diberi istilah current directory). Buat suatu GUI baru dengan nama misalnya ambil_file.
guide
Anda akan melihat pilihan mau buat GUI kosong, GUI yg pernah dibuat, atau sudah bertemplate. Pilih saja yang Blank GUI (Default). Drug toolbox command button berlambang “OK” ke arah lembar kerja GUI. Secara default akan diberi nama Push Button.

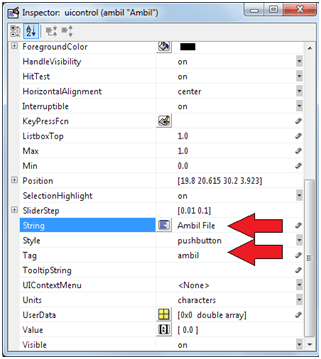
Untuk mengedit Push Button, klik ganda tombol itu hingga memunculkan properties. Ganti Push Button dengan isian pada String: Ambil File. Dan nama variabel (pada Matlab diberi nama Tag) isi dengan nama ambil. Tag ini akan menampilkan fungsi ambil di file m matlab.
Simpan GUI anda dan beri nama, misalnya ambil. Matlab akan menciptakan dua file yaitu ambil.fig dan ambil.m fungsinya berturut-turut sebagai GUI dan sebagai script. Secara ajaib, Matlab akan memberikan kode yang siap kita isi di sana. Dengan cara yang sama, buat seperti di bawah ini:

Edit text di sebelah kanan biarkan saja, tidak perlu di utak-atik supaya cepat, dan nama Tag (variabel)-nya edit1. Maksudnya adalah menampilkan nama file yang diambil. Masukan listing seperti berikut ini:
- [x,y] = uigetfile(‘*.mat’, ‘Mengambil Data’);
- set(handles.edit1,‘String’,x);
- y=load(x)
- net=y.network1
Uigetfile akan mengambil jendela get file dengan ekstensi yang akan ditampilkan *.mat. Pada jendela akan muncul nama jendela ‘Mengambil Data‘. Saya mengambil data saya bernama jst.mat, hasil training JST yang lalu. Instruksi y=load(x) akan mengambil variabel x ke workspace dan net=y.network1 mengambil variabel di y yang isinya hanya jst saya (network1). Jika Anda lihat di command window akan muncul y dan net saya, tentu saja jika Anda tidak memiliki file jst.mat milik saya tidak akan muncul networknya (coba buat sendiri). Silahkan cek apakah file tersebut muncul di sebelah kanan tombol Ambil File (Edit Text).

Sekarang kita coba menyimpan data yang kita barusan ambil (atau mungkin data hasil oleh GUI jika ada). Misal kita akan merename. Isi pada fungsi simpan (awas jangan salah kamar) di m-file pada simpan_Callback.
- y=load(‘jst.mat’)
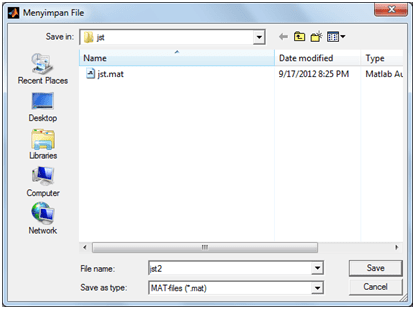
- [nm_file] = uiputfile(‘*.mat’,‘Menyimpan File’);
- data_file = [nm_file];
- save(data_file);
Jalankan, Anda akan menampilkan jendela simpan. Bisa Anda tambahkan message jika file telah tersimpan. Di sini kita coba menyimpan y hasil dari loading suatu file (‘jst.mat‘). Dan akan menyimpannya menjadi file lain, misalnya jst2.mat.
Contoh di atas hanya mencoba GUI saja, karena tidak ada yang diolah di sini. Anda bisa menyisipkan fungsi-fungsi ini pada sistem yang anda rancang. Dari pengolahan gambar hingga fungsi-fungsi berat seperti Algoritma Genetik yang saya buat untuk mencari lokasi SPBU yang optimal di Bekasi.
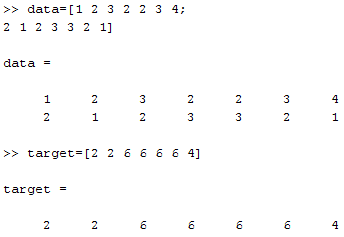


















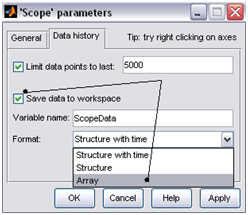







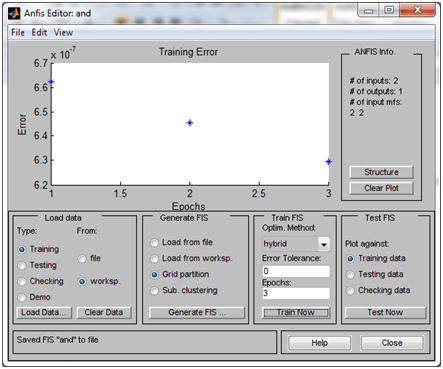
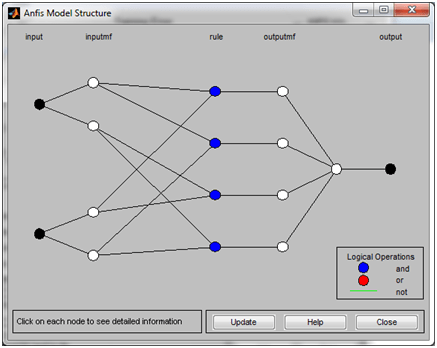
















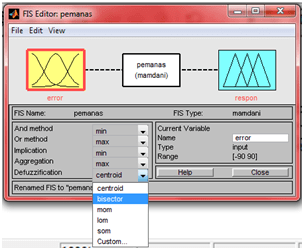
 (simulink), gambar bentuk di bawah ini, jika tidak bisa menemukan Fuzzy Logic Controller (FLC) ketik “fuzzy” di searching. Dobel klik pada “Fuzzy” di simulink, isi parameter dengan ‘pemanas.fis’ (gunakan petik satu).
(simulink), gambar bentuk di bawah ini, jika tidak bisa menemukan Fuzzy Logic Controller (FLC) ketik “fuzzy” di searching. Dobel klik pada “Fuzzy” di simulink, isi parameter dengan ‘pemanas.fis’ (gunakan petik satu).