Kategori: Information Retrieval

Mengetahui Ringkasan Video Youtube dengan Cepat

Saat ini nonton youtube terkadang lebih mudah dibanding membaca. Tapi bagi pembaca yang terbiasa membaca terkadang menonton bisa menghabiskan waktu beberapa menit hingga beberapa jam. Tentu saja ini sangat membosankan jika diminta mencari ringkasannya. Namun, saat ini perkembangan Artificial Intelligence (AI) sudah dapat mempermudah pekerjaan kita. Postingan ini bermaksud memperkenalkan Anda bagaimana cara cepat mengetahui isi video tanpa perlu menonton full link video youtube, misalnya:

Langkah pertama adalah membuka video tersebut, dilanjutkan dengan menekan view transcript di bagian bawah video tersebut. Setelah tombol ditekan maka transkript akan muncul di bawah. Berikutnya tinggal Anda kopi dan paste saja di sembarang text editor.

Anda bisa membacanya atau dengan menanyakan ChatGPT apa ringkasan atau isi dari transkrip tersebut dengan prompt> rangkum, tulisan ini tentang apa: < paste naskahnya>. Anda akan menerima jawaban yang lengkap. Selamat mencoba.

To keep running when the data is empty in Python

Machine learning is a method that involves methods with datasets. Sometimes when the dataset to be processed is empty an error will appear as below.

Several ways can be taken, but the easiest way is to check the size of the csv file. If the file size is zero Kb then it is confirmed that there is no content. Then just use the ‘if not’ instruction as sample below.


Here, the ‘os’ library is required. Don’t forget to indent the ‘if’, including the ‘else:’ side.

Contoh Deployment Python dengan PHP

Lanjutan dari pos sebelumnya, kali ini membahas praktik sederhana menjalankan hasil pemodelan Machine Learning (ML) dengan Python pada PHP. Sebenarnya Python memiliki framework Web sendiri, misalnya Flask dan Django. Namun, kebanyakan server menggunakan Apache yang berbasis PHP. Oleh karena itu perlu mengintegrasikan Python dengan Apache. Silahkan lihat tatacara untuk XAMPP di windows pada video berikut.

Untuk Linux, misal Ubuntu agak sedikit rumit karena hak akses pada file, serta environment yang agak rumit, seperti video berikut.

Video berikut menjelaskan sample deployment sentiment analysis dengan bahasa Python pada PHP-MySQL di windows.

Stopwords Removal Bhs Indonesia – via Sastrawi

Dalam text processing, selain menghilangkan karakter-karakter non bahasa seperti hashtag, website symbols, dan lain-lain, perlu juga menghilangkan stopwords yang merupakan kata yang kurang bermakna untuk diproses karena hampir di setiap berkas ada, misalnya ‘dan’,’atau’, ‘untuk’, dan lain-lain. Bayangkan misalnya kita searching di Google dengan kata kunci ‘A dan B’ maka kata ‘dan’ tentu saja tidak perlu di-searching karena hampir semua dokumen ada kata itu.

Natural Language Processing (NLP) merupakan bidang ilmu komputer yang fokus ke bahasa, sehingga mau tidak mau antara satu bahasa dengan bahasa lain pasti berbeda. Untuk bahasa Inggris, Natural Language Toolkit (NLTK) pada library Scikit Learn sudah lama ada, sementara untuk bahasa Indonesia, tersedia library Sastrawi yang dapat digunakan untuk menghilangkan Stopwords, selain tentu saja untuk Stemming dalam menghilangkan imbuhan (awalan, sampiran dan akhiran). Lebih lengkapnya dapat dilihat pada video berikut.

Inverted Index dengan Google Colab – Python

Beberapa buku teks memiliki index yang diletakan di akhir buku. Isi index adalah kata-kata penting beserta halaman dimana kata tersebut berada. Biasanya kata-kata tersebut disebutkan lebih dari satu halaman.

Sementara itu ketika seseorang mengetikan kata di mesin Google, misalnya “American Revolution”, maka Google akan mencari di mana saja kata tersebut berada, misalnya pada Index di gambar di atas di halaman 84,98, dan 166. Karena diletakan di muka yang mirip daftar isi, maka di situlah kata “inverted” bermula, yang seharusnya di belakang tapi di muka sebagai alat pencari. Sebagai contoh, puisi “Aku” karya Chairil Anwar berikut. Anggap saja satu line/baris merupakan satu berkas dokumen, atau kalau dalam satu buku adalah halaman.

  • Doc 1.Kalau sampai waktuku
  • Doc 2.’Ku mau tak seorang ‘kan merayu
  • Doc 3.Tidak juga kau
  • Doc 4.Tak perlu sedu sedan itu
  • Doc 5.Aku ini binatang jalang
  • Doc 6.Dari kumpulannya terbuang
  • Doc 7.Biar peluru menembus kulitku
  • Doc 8.Aku tetap meradang menerjang
  • Doc 9.Luka dan bisa kubawa berlari .. Berlari
  • Doc 10.Hingga hilang pedih peri
  • Doc 11.Dan aku akan lebih tidak peduli
  • Doc 12.Aku mau hidup seribu tahun lagi!

Aslinya sih satu dokumen itu satu berkas berupa buku pdf, postingan internet, jurnal, dll, tapi di sini dianggap satu baris/line saja. Atau bisa juga sih, satu berkas tersebut dijadikan satu baris dengan doc-id sebagai penunjuk line/baris berkas itu. Kalau forward index membuat index dari konten, inverted index memetakan kata/istilah ke konten. Kita memanfaatkan inverted index Google yang setiap hari membuat index (forward index) dari data yang di crawler di seluruh dunia. Berikutnya, untuk praktik siapkan sebuah file txt yang berisi puisi di atas, atau contoh sembarang. Buka Google Colab dan upload file tersebut.

Silahkan lihat kode di referensi di akhir postingan ini. Jika dijalankan, dihasilkan inverted index seperti di bawah ini. Cek apakah benar beberapa kata tepat berada di dokumen/line pada file “Aku.txt” di atas.

Di sini kita tinggal memasukan frekuensi, misalnya ‘berlari’ itu ada dua kali. Untuk jelasnya silahkan lihat video tutorial saya berikut ini.

Ref:

Link: geeksforgeeks.org/create-inverted-index-for-file-using-python/

Menghitung Jumlah Kata dengan Python

Menghitung jumlah kata merupakan tugas wajib yang harus bisa diselesaikan oleh mesin pengelola teks. Teknik telah digunakan oleh word processing misalnya MS Word. Ketika kita mengetik, di bagian bawah langsung tercetak jumlah kata yang telah diketik. Nah, di sini kita coba teknik yang digunakan dalam bahasa pemrograman Python.

Library yang digunakan untuk menghitung kata adalah collections yang memiliki satu fungsi bernama Counter. Gunakan instruksi Open untuk mengambil file txt yang akan dikelola.

  • f2 =  open(‘Praktek.txt’, ‘r’)
  • content = f2.read()
  • print(content)

Variabel content ketika di-print akan menampilkan isi dari file “Praktek.txt” seperti praktek sebelumnya (lihat pos yang lalu). Tetapi kali ini kita menggunakan fungsi split untuk memisahkan kata dari file tersebut.

  • words = open(‘Praktek.txt’).read().split()
  • words

Terakhir kita menggunakan fungsi Counter baik untuk menampilkan jumlah per kata maupun jumlah total kata (dengan fungsi len).

Untuk jelasnya lihat video tutorial ini.

Konversi Huruf Besar dan Huruf Kecil Pada Python (Google Colab)

Untuk mengolah teks diperlukan proses konversi ke huruf kecil semua sebelum diolah lebih lanjut seperti stemming, pencarian kata dasar, dan operasi pada teks lainnya. Gunakan sembarang file txt untuk praktek yang diunggah ke Google Colab.

  • f2 = open(‘Praktek.txt’, ‘r’)
  • content = f2.read()
  • print(content)

Perhatikan di sini fungsi open memiliki parameter ‘r’ yang berbeda dengan post yang lalu (tanpa parameter ‘r’). Di sini ketika berganti baris, teks tidak ditulis dalam kode \n melainkan berganti baris.

Gunakan fungsi “upper” atau “lower” untuk beruturut-turut merabah seluruh teks menjadi huruf besar atau huruf kecil semua.

  • content.upper()

Sebagai penutup, ada satu fungsi split untuk memisah teks tersebut menjadi kata per kata ke bawah dengan kode sebagai berikut.

  • list_ = open(“Praktek.txt”).read().split()
  • list_

Ini merupakan teknik menghitung berapa jumlah kata yang ada dalam satu paragraph.

Untuk lebih jelasnya simak video berikut ini:

Mengimpor Teks di Google Colab

Google colab merupakan fasilitas pemrograman Python yang disediakan secara online oleh Google. Untuk mengaksesnya silahkan kunjungi: https://colab.research.google.com/. Sebagai bahan praktek, siapkan sebuah file teks, misalnya Praktek.txt yang dapat Anda buat secara kilat dengan text editor, misalnya notepad.

Buat notebook baru dengan file – New Notebook di Google Colab. Jika Anda lihat gambar di atas ada fasilitas Files yang harus Anda buka dulu dengan menekan simbol “File” di kiri bawah gambar di atas. Setelah fasilitas file muncul, tekan simbol “Upload” berupa gambar panah ke atas untuk mengupload sembarang file txt.

Perhatikan di jendela Code Anda bisa menyisipkan kode. Salah satu keunggulan notebook adalah bisa memisahkan kode menjadi beberapa sel terpisah yang bisa dirun sendiri-sendiri. Kata kunci “open” dan “read” di atas muncul ketika satu huruf ditekan. Sangat membantu bagi yang kurang hafal instruksi-instruksi Python.

Silahkan lihat video berikut untuk lebih jelasnya. Salam.

 

Instal Plug-in TwitterStreamImporter di Gephi Untuk Scrap Twitter Langsung

Twitter dapat dimanfaatkan untuk mencari tahu akun mana yang aktif membicarakan topik tertentu. Salah satu aplikasi tak berbayar yang mampu men-scrap (istilah mengambil data) Twitter adalah Gephi. Biasanya scrap menggunakan bahasa pemrograman tertentu, tetapi perlu usaha untuk membuat networknya. Nah, Gephi memiliki kemampuan selain men-scrap juga membuat networknya.

Menambahkan Plug-In

Buka Gephi dan masuk ke menu Tools – Plug-In. Banyak fasilitas yang tersedia, salah satunya yang akan digunakan kali ini adalah TwitterStreamImporter.

Cari di tabel Plug-In dan ceklis ketika plugin tersebut ditemukan. Tekan Install untuk melakukan proses instalasi plugin TwitterStreamImporter. Tunggu beberapa saat hingga proses pengunduhan dan instalasi selesai.

Agar memiliki efek ada baiknya memilih Restart Now ketika muncul pilihan pada jendela “Plugin Installer”. Gephi akan shutdown dan muncul kembali dengan fasilitas tambahan yaitu “plugin” yang baru saja kita install.

Ciri-ciri Plugin telah terinstal adalah di bagian kiri bawah muncul tab “Twitter Streaming Importer”. Nah selanjutnya kita tinggal melakukan langkah: 1) Set Credentials, 2) Define the Query.

Silahkan lihat postingan yang lalu untuk mendaftarkan Credential twitter. Postingan berikutnya akan berlanjut menscrap data dengan plugin tersebut sekaligus analisanya dengan Gephi. Sekian, semoga bermanfaat.

Nucoll dan Gephi Untuk Profiling Twitter

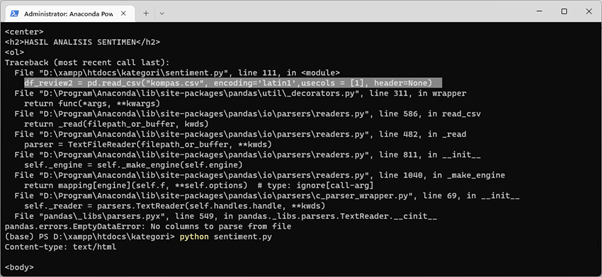
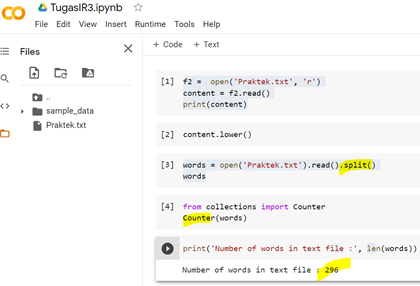
Profiling terkadang diperlukan ketika ingin mengetahui informasi seseorang misalnya calon pegawai, caleg, dan sebagainya. Mula-mula dilakukan secara manual lewat searching di media sosial. Namun ketika teknologi kian berkembang, banyak aplikasi-aplikasi tersedia untuk membantu proses profiling, salah satunya nucoll dan Gephi.

Nucoll

Nucoll merupakan aplikasi versi baru dari Tweecoll yang banyak dikeluhkan karena tidak mudah berjalan di Windows. Nucoll dapat diunduh programnya di link resminya berikut ini (sesuaikan dengan sistem operasi Anda). Aplikasi ini hanya berisi EXE saja dan dijalankan menggunakan konsol Python.

Untuk menghasilkan file yang akan dilihat network-nya diperlukan tiga langkah sesuai dengan instruksi pada gambar di atas:

  • nucoll init <akuntwitter>
  • nucoll fetch <akuntwitter>
  • nucoll edgelist <akuntwitter>

Terdapat file berekstensi dat, gml, dan qry (jika menggunakan fungsi tweets). Hasil yang akan dikirim ke Gephi adalah file berekstensi GML di folder kerja. Berikutnya perlu menginstall Gephi. Sebagai informasi, jika akun twitter yang akan dicari memiliki banyak follower, dibutuhkan proses yang lumayan lama.

Gephi

Gephi sering digunakan untuk mendeteksi network pengguna twitter. Aplikasi ini dapat diunduh di link berikut. Banyak yang sudah menerapkan, salah satunya adalah drone emprit.

Ketika tulisan ini dibuat, sudah masuk versi 0.9.2. Aplikasi Gephi dibuat dengan menggunakan bahasa Java.

Ikuti saja instruksinya hingga proses selesai. Tunggu beberapa saat hingga selesai.

Berikutnya jalankan Gephi untuk menampilkan network yang berasal dari Nucoll. Buat satu project baru. Impor file GML dari nucoll lewat menu file – open.

Ketika file GML hasil scrapping dengan nucoll diimpor, akan muncul network di Gephi. Tekan simbol “T” di bagian bawah untuk melihat labelnya.

Silahkan yang tertarik bisa melihat tutorialnya di link berikut ini. Banyak fasilitas-fasilitas lain (pewarnaan, indikator-indikator dan sebagainya). Oiya, silahkan gunakan fugnsi “tweets” dari Nucoll untuk men-scrap tweets seseorang. Selamat mencoba, semoga bermanfaat.

NOTE: Untuk menjalankan Nucoll perlu mendaftarkan Consumer Key (lihat post terdahulu).

Menganalisa Akun Twitter – Mendapatkan Keys & Token Twitter API

Twitter menyediakan API untuk mengunduh tweets seseorang. Walaupun yang tepat istilahnya “wrapper” bukan Application Programming Interface (API). Langkah pertama, tentu saja harus punya akun Twitter dulu. Berikut langkah-langkah yang perlu dilakukan.

Mendaftar Sebagai Developer

Pertama-tama masuk ke situs https://developer.twitter.com/ setelah login Twitter di browser, misalnya Mozilla. Atau langsung saja ke sini untuk membuat application baru: https://developer.twitter.com/en/apps. Tekan Create Account untuk membuat app baru.

Tiap saat sepertinya peraturan berubah-ubah. Ketika tulisan ini dibuat harus meng-apply akun sebagai developer.

Kemudian muncul pesan untuk verifikasi via nomor handphone. Tekan Add a valid phone number.

Setelah memasukan nomor ponsel yang sesuai, tunggu sms dari twitter untuk memasukan nomor verifikasi. Setelah meinginput nomor tersebut, maka phone number kita sudah terverifikasi. Tekan Continue. Berikutnya pilih perorangan atau organisasi app yang akan digunakan. Ada pertanyaan yang agak sulit mengenai mengapa membutuhkan API? Serta untuk apa dan metode apa yang digunakan nanti. Nah di sini kita diminta menjawab dengan gaya “mengarang bebas” karena diminta menulis jawaban lebih dari 300 kata. Akhiri dengan menekan Accept setelah membaca (kalau sempat) Term of Service.

Jangan lupa menceklis kotak di bagian bawan TOS. Selanjutnya diminta membuka email dari akun kita. Jika sudah ada pesan masuk dari Twitter, tekan konfirmasi.

Selesai sudah mendaftar sebagai developer yang menggunakan fasilitas Twitter. Pastikan akan masuk ke jendela developer https://developer.twitter.com/en/account/get-started.

Mendapatkan Twitter API Key

Setelah terdaftar sebagai developer berikutnya adalah membuat app. Di bagian dashboard tekan Apps dan jika tidak ada akan muncul tombol Create an App. Cukup banyak yang harus diisi, tetapi ikuti saja sampai selesai, terutama yang required harus diisi. Jika sudah maka terakhir konfirmasi kembali. Di sini beberapa kali ditolak karena nama aplikasi sudah ada yang punya, akhirnya setelah diganti, misalnya “kepo_movie”, baru lah bisa, hehe.

Keys and tokens inilah yang akan digunakan untuk aplikasi meneliti tweets dari sebuah akun twitter. Langkah selanjutnya adalah memilih aplikasi untuk analisa tweeter, misalnya Tweepy yang terkenal bagi programmer Python. Selamat mencoba, semoga peraturan Twitter masih seperti ketika tulisan ini dibuat.

Sumber Belajar Pemrosesan Teks dan Perolehan Informasi

Saat ini informasi sangat mudah didapat karena era Big Data dengan konsep 5V-nya (Velocity, Veracity, Volume, Value, dan Variability). Walaupun bagi praktisi Big Data ada konsep “data yang buruk lebih baik daripada tidak ada data” tetapi bagi pelajar dan mahasiswa, dibutuhkan sumber-sumber yang memang dibutuhkannya. Banyak ebook-ebook berkualitas baik banyak dijumpai di internet baik lewat situs sharing ataupun via media sosial seperti Whatsapp. Namun toh, para mahasiswa kurang begitu berminat membacanya (bahkan saya pun agak malas ..). Tapi ya, kalo bisa sih dibaca sampai habis.

Untuk pemrosesan teks, text mining, atau perolehan informasi salah satu buku andalannya adalah terbitan MIT press (C. Manning) dengan teori-teori dasarnya. Ada juga buku karangan Banch tentang Text Mining dengan praktek aplikasinya dengan Matlab. Kebanyakan karena saking “dasanya” jadi sulit untuk diterapkan langsung seperti bagaimana implementasinya di search engine seperti Google atau Bing.

Berbicara mengenai search engine, bagi mahasiswa atau saya juga, yang ingin belajar cepat sekelebat karena limit waktu yang terbatas, Google dkk menjadi andalan utama setelah situs-situs diskusi di internet. Modal dasar yang harus dimiliki tentu saja kemampuan berbahasa Inggris. Walaupun ada translate google, tetap harus bisa bahasa Inggris jika tidak ingin repot bolak-balik buka kamus.

Ada proyek-proyek online yang beredar di internet, salah satunya adalah situs ini yang menyediakan contoh sample data yang akan diolah.

Bagaimana cara mengolahnya? Silahkan download buku Text Mining with Matlab karya Banch, atau datang ke situs-situs diskusi, misalnya tentang pembuatan model bahkan membuat mesin yang bisa membuat sebuah kalimat dengan beberapa kata kunci.

Saya sempat mencobanya. Pertama-tama dengan Matlab 2008. Ternyata dengan versi tersebut banyak masalah yang dijumpai karena sudah tertinggal jauh. Silahkan gunakan yang terkini. Beberapa fungsi m-file perlu diunduh agar bisa berfungsi, dan lumayan bisa dipakai untuk mengutak-atik teks. Mungkin pembaca punya alternatif lain yang lebih baik, silahkan ber-komentar. Yuk, belajar text mining.

Mengambil File Microsoft Word dan Indexing Pada Matlab

[inf.retrievalt.komputer|lab.software|pert.9]

Salah satu langkah perolehan informasi yang penting adalah pembuatan indeks. Indeks merupakan salah satu kunci untuk pencarian informasi. Untuk menghasilkan pengindeks yang baik perlu menggunakan teknik-teknik yang ada pada pemrosesan teks. Postingan kali ini bermaksud mengetahui cara pembuatan indeks dengan file yang diambil dari microsoft word.

Mengambil File Ms Word

Banyak informasi yang memberikan cara bagaimana mengambil file word agar bisa diproses lebih lanjut pada Matlab. Biasanya file yang langsung bisa digunakan adalah file berekstensi txt, namun karena banyaknya file berformat DOC atau DOCX maka perlu mengetahui cara pengambilan file bertipe itu agar bisa diolah lebih lanjut pada Matlab. Agar lebih nyaman, ada baiknya membuat Graphic User Interface (GUI) agar lebih mudah digunakan atau disimpan agar mudah digunakan nantinya.

Masuk ke callback Ambil File dan isikan kode berikut menggunakan uigetfile yang mengeluarkan form ambil file. Akhiri dengan membuat variabel agar bisa digunakan nantinya lewat mekanisme handles.

  • [a,b]=uigetfile(‘*.docx’)
  • handles.a=a;
  • handles.b=b;
  • guidata(hObject,handles)

Sementara pada callback Pra-Proses diisi dengan kode-kode berikut dimulai dari mengambil data dari word:

  • word = actxserver(‘Word.Application’);
  • file=strcat(handles.b,handles.a)
  • wdoc = word.Documents.Open(file);
  • sometext = wdoc.Content.Text;

Variabel “file” merupakan string yang diambil dari instruksi “uigetfile” pada pushbutton sebelumnya yang kemudian disimpan dalam variabel sometext. (Lihat penjelasannya di buku Text Mining dengan Matlab karya Bachs).

  • temp = sometext
  • temp = lower(temp)
  • temp = regexprep(temp,'</verse>’,’ S ‘)
  • temp = regexprep(temp,'<.*?”‘,”)
  • temp= regexprep(temp,’ ‘,”’,”’)
  • temp = regexprep(temp,’\W’,’ ‘)
  • temp = strtrim(regexprep(temp,’\s*’,’ ‘))
  • temp=regexprep(temp,’ ‘,”’,”’)
  • eval([‘wordsofverses={”’,temp,”’};’]);
  • limits = [0,find(strcmp(wordsofverses,’S’))]
  • for k=1:length(limits)-1
  • verses(k).vocab = unique(wordsofverses(limits(k)+1:limits(k+1)-1));
  • end;

Variabel “temp” berisi hasil pemrosesan yang dimulai dari lower untuk mengecilkan seluruh huruf hingga mengkonversi string word tersebut menjadi cell dalam variabel wordsofverses. Hasilnya kira-kira sebagai berikut. Semoga bermanfaat.

Fixing: “Warning: Single line Edit Controls can not have multi-line text”

[inf.retrieval|t.komputer|lab.soft|pert.8]

This problem appears when someone tries to send the result to edit text. The warning is shown in command window and the edit text in GUI is also disappeared. First we should understand that Matlab has two kinds of text format: string and cell. The cell cannot be presented, except you transpose it. But the edit text will show the text in column based. Only the string/char format can be presented in row based (see the picture below showing the string and cell).

Some text processing methods need conversion from string to cell. Therefore, the manipulation should be done in order to show the text in edit text. The algorithm are as follow:

  • Input: cell
  • Output: string in row
  • Use function char to convert cell into character
  • Transpose the characters
  • Use function sprintf to print the characters in row based

This simple method can be solve the warning above. As an impormation, some text manipulation need conversion from cell to char and vice versa, e.g. regexp (regular expression function). I hope this information is useful. This is an output when I stemmed to remove preffix (‘ber’) except when the root-word below 4 characters (e.g. “dua” from “berdua”)

Stemming Pada Matlab

[per.informasi|t.komputer|lab.soft|pert.5]

Jika pada pertemuan sebelumnya telah berhasil memisahkan kata-kata dalam suatu kalimat agar bisa menghitung jumlah katanya maka pada pertemuan kali ini akan mencoba memisahkan kata dari imbuhan (awalan dan akhiran) agar diperoleh kata dasarnya yang dikenal dengan istilah stemming/lematization. Proses ini sangat penting dalam perancangan mesin pencari (searching). Imbuhan merupakan ciri khas bahasa Indonesia yang memang berbeda sekali dengan bahasa Inggris. Coba rancang GUI berikut untuk melakukan proses stemming.

Imbuhan ada banyak misalnya me, meng, ber, per, -an, dan lain-lain. Untuk memisahkannya kita perlu memproses pencarian berdasarkan spasi dan titik (untuk akhiran). Jika tanpa spasi akan terjadi kesalahan karena sistem akan mereplace seluruh yang diduga awalan/akhiran walau terletak di tengah-tengah kata yang tentu saja salah.

  • % menghilangkan “-an”
  • y=regexprep(y,‘an+\s’,‘ ‘) % sebelum spasi
  • y=regexprep(y,‘an+\.’,‘.’) % sebelum titik
  • set(handles.edit1,‘String’,y)

Kode di atas bermaksud menghilangkan akhiran –an. Jika diinput kata “akhiran.” Akan dihasilkan kata dasarnya “akhir”. Ada dua deteksi yaitu sebelum spasi dan sebelum titik.

Logika sederhananya adalah mengganti “-an” tersebut dengan “blank”. Fungsi yang digunakan adalah regexprep yang mencari dan me-replace suatu string. Pertemuan berikutnya akan menggunakan proses perhitungan karakter tertentu, misalnya “makan”, tidak bisa jadi “mak” karena kurang dari 4 karakter. Selain itu perlu proses N-gram (dua, tiga, dst). Selamat mencoba, semoga UTS dapat dikerjakan dengan baik.