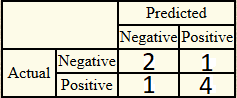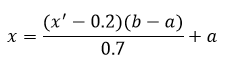[peng.citra|t.kom|lab.hardware|pert.7]
Warna dasar RGB adalah Red, Green, dan Blue yang masing-masing menyatakan nilai maksimal komposisinya yaitu 255. Misalnya warna merah, maka matriks-nya sebesar [255 0 0], begitu juga untuk warna hijau dan biru, masing-masing [0 255 0] dan [0 0 255]. Bagaimana cara mendeteksi warna-warna komposit yang bukan merupakan warna dasar seperti kuning, jingga, dan lain-lain? Postingan kali ini sedikit menjelaskan cara mendeteksinya dengan menggunakan jarak Euclidean.
Standar Warna RGB
Standar warna RGB banyak diterapkan pada image processing. Standar ini menggunakan warna merah, hijau dan biru sebagai patokan warna-warna lainnya. Warna lainnya dapat dibuat dengan menggabungkan proporsi warna merah, hijau, dan biru tersebut. Berikut standar warna selain merah, hijau, dan biru.
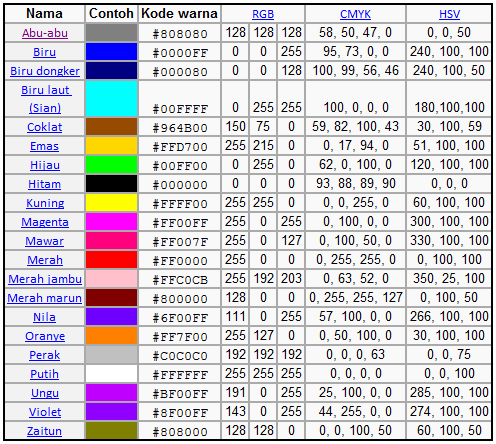
Tabel di atas juga menyertakan paduan standar Cyan, Magenta, Yelow, dan Black (CMYK) dan HSV. Sebagai kelanjutan Pert 6 yang lalu, di sini kita menerapkan deteksi warna dengan jarak Euclidean.
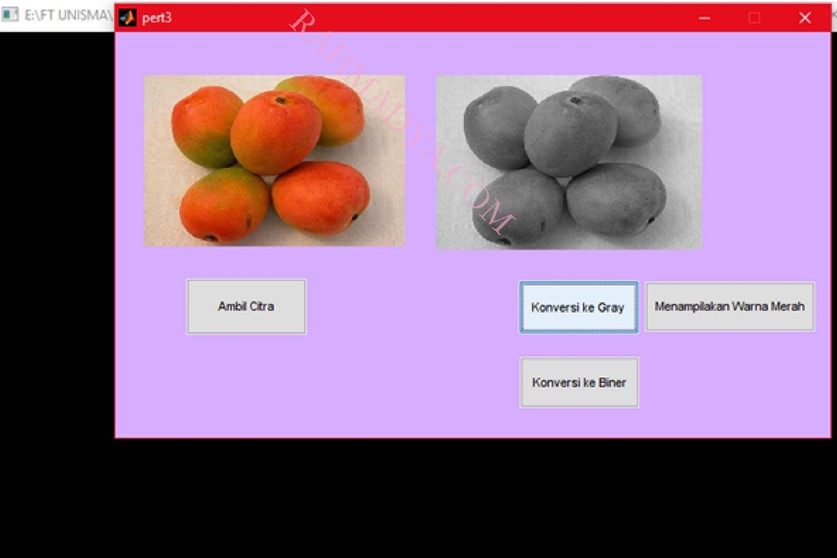
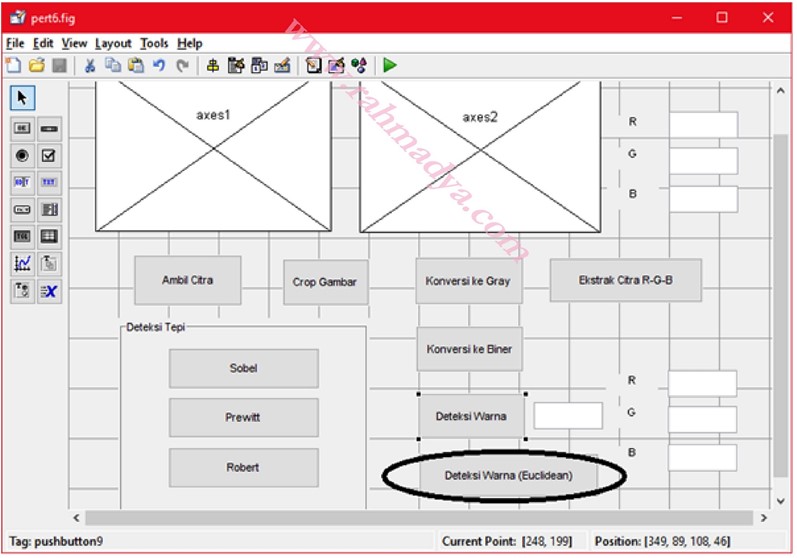
Praktek dengan GUI
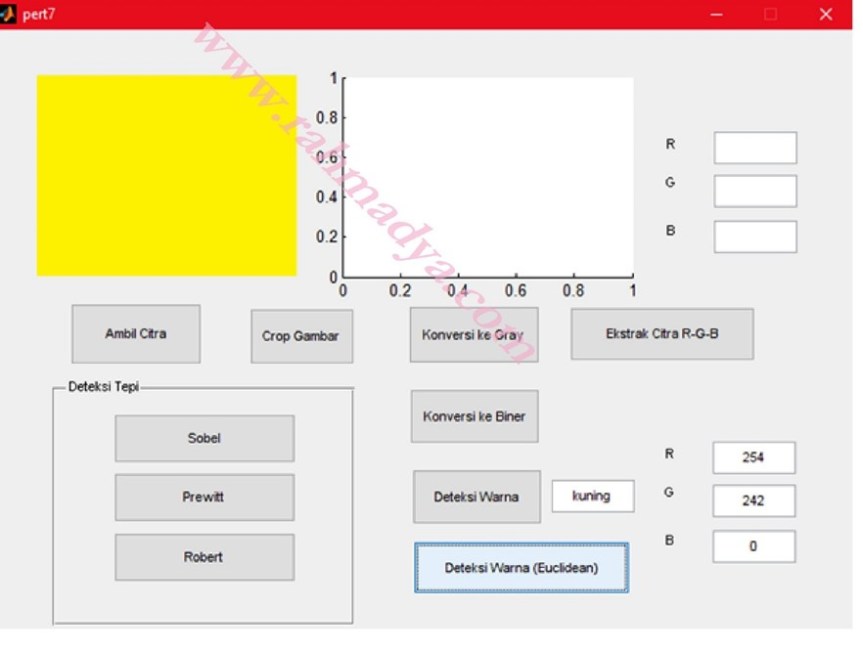
Tambahkan kode tambahan di tombol deteksi warna (Euclidean) karena bukan hanya R, G, dan B, melainkan beberapa warna lain misalnya kuning, oranye, dan hitam.

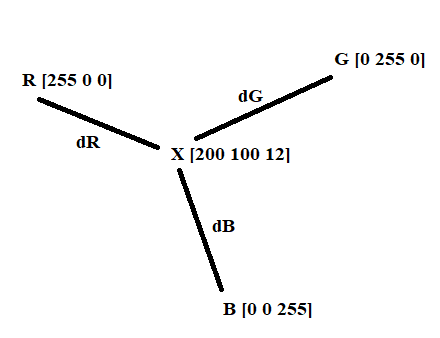
Tambahkan tiga jarak baru yaitu dY, dO, dan dK untuk jarak terhadap kuning, oranye dan hitam. Untuk memudahkan penentuan jarak terdekat gunakan fungsi min disertai dengan indeksnya. Indeks dapat diketahui dengan membuat sebuah vektor berisi warna-warna dari merah hingga hitam. Sehingga ketika nilai minimum diketahui, diketahui pula indeksnya. Warna dapat diketahui berdasarkan indeks-nya dari vektor warna.
- …
- dR=norm(warna-[255 0 0])
- dH=norm(warna-[0 255 0])
- dB=norm(warna-[0 0 255])
- dY=norm(warna-[255 255 0])
- dO=norm(warna-[255 127 0])
- dK=norm(warna-[0 0 0])
- hasil=[dR dH dB dY dO dK]
- % mencari jarak terkecil
- strwarna={‘merah’
‘hijau’
‘biru’
‘kuning’
‘jingga’
‘hitam’}
- [minimum,indeks]=min(hasil)
- outwarna=strwarna(indeks)
- set(handles.edit4,‘String’,outwarna)
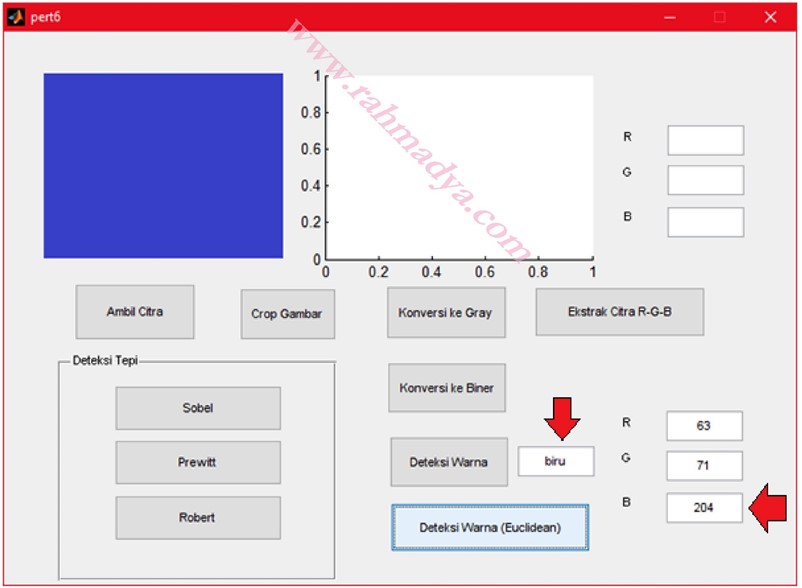
Coba uji dengan memasukan data sesuai warnanya, misalnya kuning, oranye dan hitam. Coba uji pula dengan warna yang tidak terlalu hitam (abu-abu), atau tidak terlalu kuning. Sistem akan mencoba mendekati dengan warna-warna standar yang ada (R,G,B, plus kuning, orange dan hitam). Semoga bermanfaat.







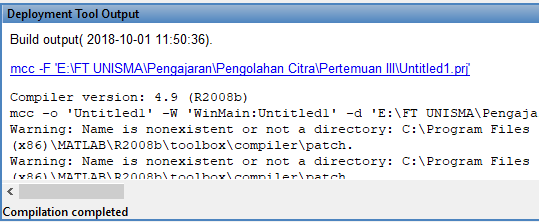
 di bagian atas. Setelah itu masuk ke command window untuk memasukan beberapa parameter yang dibutuhkan Matlab untuk membangun/build program. Tekan mbuild_setup di bawah command window.
di bagian atas. Setelah itu masuk ke command window untuk memasukan beberapa parameter yang dibutuhkan Matlab untuk membangun/build program. Tekan mbuild_setup di bawah command window.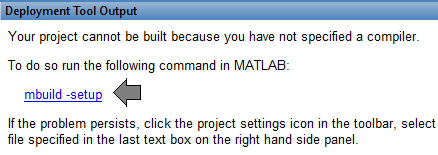
 dan pastikan muncul instruksi di bawah:
dan pastikan muncul instruksi di bawah: