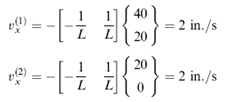Sehubungan ada masalah dengan kampus (UAS yang diundur, banjir, dll), maka UAS Aljabar kali ini terjadi perubahan soal dari praktek menjadi teori. Soal sesuai dengan NPM masing-masing yang harus dikerjakan dengan metode klasik (operasi baris) eliminasi Gauss.
Kategori: Unisma
UAS Aljabar Linear
Aljabar Linear. 03.01.2013. Teknik Komputer
Akhirnya kita sampai pada pertemuan terakhir, yaitu membahas materi yang akan diujikan pada Ujian Akhir Semester (UAS) nanti. Karena ada pemisahan kelas menjadi dua kelas (kelas selasa dan kamis), dan ada perbedaan jumlah nilai tugas harian akibat banyaknya libur di hari selasa, untuk menyamakan dengan kelas Kamis, maka untuk kelas SELASA, saat UAS nanti diharapkan mengumpulkan tugas perkalian matriks dengan Java Script. Tugas merupakan tugas satu kelas, tetapi jika ada siswa yang merasa tidak puas dengan jawaban kelas dapat mengumpulkan tugas sendiri atau berkelompok. Tugas perkalian matriks dikerjakan dengan mencontoh tulisan saya sebelumnya tentang penjumlahan matriks (Membuat Matriks dengan Java Script) dengan mengganti bagian penjumlahan dengan perkalian. Sementara itu, algoritma untuk perkalian dapat kalian perhatikan tulisan Mengalikan Matriks 3 x 3 dengan mengurangi bagian I,j, dan c dari 3 menjadi 2.

Soal UAS berkisar seputar mencari invers matriks dengan menggunakan manipulasi baris yang dikenal dengan nama eliminasi Gauss. Perhatikan tulisan Mencari Invers dengan Operasi Baris dan coba latihan dengan angka yang lain, uji jawabannya dengan Matlab lewat fungsi INV. Jangan lupa syarat suatu matriks dapat dicari inversnya adalah determinannya nol. Tiap siswa kemungkinan besar berbeda matriks yang ada pada soal karena soal berdasarkan NIM masing-masing. Sifat ujian buku terbuka, bawa perlengkapan seperlunya seperti pulpen (jangan pensil ya, nggak jelas), kalkulator, dan lain-lain, juga tidak perlu acara bakar ban J.
Membuat Master Slide pada Power Point
Materi UAS Komputer I. 03.01.2013. Tek. Elektronik
Terkadang kita membutuhkan suatu template pada slide yang akan kita buat agar seragam dari mulai hingga selesai. Untuk mudahnya kita buat tulisan PANCASILA dengan tiap SILA dalam satu SLIDE. Buka Power Point. Masuk ke View dan Klik Slide Master.

Setelah masuk ke mode Slide Master, tampak di barisan bawah jenis slide yang akan dirubah seting template-nya. Misal kita akan atur yang ketiga dari atas. Klik template slide tersebut.

Kemudian Anda bebas mengatur template tersebut, misalnya Warna, background, tulisan, logo, dan sebagainya. Coba buat mirip seperti ini, karena akan kita masukan hiperlink yang akan menghubungkan judul ke slide tertentu. Buat judul PANCASILA di bagian Judul, buat background yang Anda sukai, tambahkan Text Box yang akan menjadi Hyperlink ke slide yang dituju.

Untuk mempercepat, text box dapat di Copy-paste saja dari yang sebelumnya. Ganti menjadi tulisan Sila pertama hingga kelima. Jika sudah selesai, tekan tombol  untuk kembali ke mode edit slide. Selanjutnya, ketika Anda membuat slide baru lewat menu New Slide, akan tampak template yang baru saja kita atur.
untuk kembali ke mode edit slide. Selanjutnya, ketika Anda membuat slide baru lewat menu New Slide, akan tampak template yang baru saja kita atur.

Buat Tulisan tiap sila untuk tiap SLIDE dari sila pertama hingga sila kelima. Manfaat dari membuat slide baru dari slide master adalah ketika Master dirubah, maka seluruh slide akan ikut berubah, Misalnya kita akan tambahkan LOGO pada slide Master, maka seluruh slide yang dibuat dari master tersebut akan muncul logonya. Berikutnya kita akan membuat Hyperlink yang mengarahkan link sila ke isi sila pada slide pertama hingga kelima. Klik Insert – Hyperlink. Sorot Sile Pertama, ketika muncul jendela Insert Hyperlink pilih Place in The Document karena link yang dituju masih dalam file yang sama. Anda bisa saja menambah link internet, atau file lainnya.

Lakukan hal yang sama untuk sila kedua hingga kelima. Jalankan dengan Slide Show, pastikan ketika Anda mengklik Sila Kedua, di sebelah kanan akan muncul tulisan Kemanusiaan yang Adil dan Beradab.
Membuat Matriks dengan Java Script
Aljabar Linear. 31.12.2012. Teknik Komputer
Untuk materi UAS nanti berikut ini teknik membuat matriks dengan Java Script setelah pada pertemuan yang lalu membuat vektor. Berbeda dengan vektor, Matriks masuk dalam kategori array multi dimensi. Kode berikut ini menunjukkan penjumlahan matriks A dan B yang berukuran 2×2 menjadi Matriks C.
<HTML>
<HEAD>
<TITLE>Membuat Matriks
</TITLE>
<SCRIPT LANGUAGE = “JavaScript”>
</SCRIPT>
</HEAD>
<BODY>
<SCRIPT LANGUAGE = “JavaScript”>
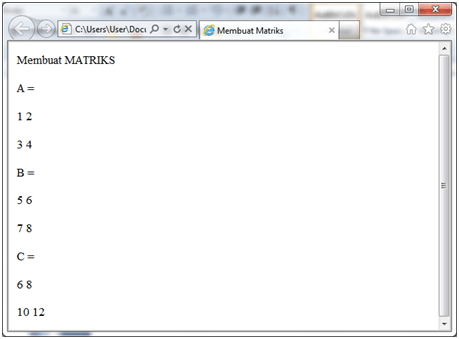
document.writeln(“Membuat MATRIKS”)
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
document.writeln(” A = “)
var a = new Array (2);
a[0]=new Array(2);
a[1]=new Array(2);
a[0][0]=1;a[0][1]=2;a[1][0]=3;a[1][1]=4;
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
document.writeln(a[0][0])
document.writeln(a[0][1])
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
document.writeln(a[1][0])
document.writeln(a[1][1])
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
var b = new Array (2);
b[0]=new Array(2);
b[1]=new Array(2);
b[0][0]=5;b[0][1]=6;b[1][0]=7;b[1][1]=8;
document.writeln(” B = “)
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
document.writeln(b[0][0])
document.writeln(b[0][1])
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
document.writeln(b[1][0])
document.writeln(b[1][1])
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
document.writeln(” C = “)
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
var c = new Array (2);
c[0]=new Array(2);
c[1]=new Array(2);
for (var i=0; i<2; i++)
for (var j=0; j<2; j++)
c[i][j]=a[i][j]+b[i][j];
document.writeln(c[0][0])
document.writeln(c[0][1])
document.writeln(“<PRE>”)
document.writeln(“</PRE>”)
document.writeln(c[1][0])
document.writeln(c[1][1])
</SCRIPT>
</BODY>
</HTML>
Simpan dengan ekstensi .htm pada notepad atau text editor lainnya. Coba buat perkalian matriks dengant teknik seperti pada bahasa pemrograman C/C++. NOTE: ketik ulang tanda petik “” jika co-pas dari blog ini.
Membuat Vektor dengan Java Script
Aljabar Linear. 27.12.2012. Tek Komputer
Java Script merupakan salah satu bahasa berbasis web yang banyak digunakan oleh programmer. Oleh karena itu kita coba membuat vektor dengan Java Script. Metode yang kita gunakan adalah dengan membuat variabel array. Misal kita akan membuat vektor a dengan isi 1,2, dan 3. Gunakan listing berikut:
<HTML>
<HEAD>
<TITLE>Membuat Vektor
</TITLE>
<SCRIPT LANGUAGE = “JavaScript”>
</SCRIPT>
</HEAD>
<BODY>
<SCRIPT LANGUAGE = “JavaScript”>
document.writeln(“Membuat Vektor”)
document.writeln(“<PRE>”);
document.writeln(” A = “)
var a = new Array (1,2,3);
for (var i = 0; i < 3; i++)
document.writeln(a[i])
</SCRIPT>
</BODY>
</HTML>
Buat dengan notepad, jangan lupa ketika menyimpan ekstensinya beri nama .htm. Jika sudah berjalan normal, coba buat matriks. Matriks merupakan array multidimensi (lebih dari satu dimensi). Untuk input data secara interaktif, gunakan prompt pada kode programnya.
<HTML>
<HEAD>
<TITLE>Membuat Vektor
</TITLE>
<SCRIPT LANGUAGE = “JavaScript”>
</SCRIPT>
</HEAD>
<BODY>
<SCRIPT LANGUAGE = “JavaScript”>
document.writeln(“Membuat Vektor”)
document.writeln(” A = [“)
var a = new Array (10);
for (var i = 0; i < 10; i++)
a[i]=prompt(“Masukan Vektor”)
for (var i = 0; i < 10; i++)
document.writeln(a[i])
document.writeln(” ]”)
</SCRIPT>
</BODY>
</HTML>
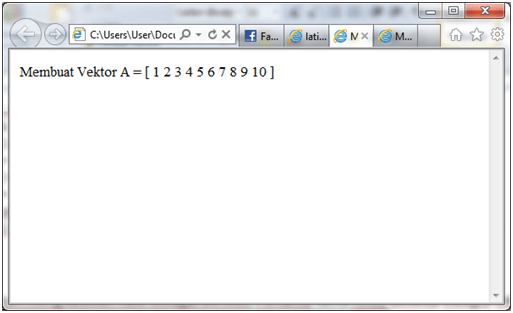
Jika disimpan dan dijalankan menghasilkan hasil sebagai berikut. Pertama-tama Anda diminta mengisi vektornya:

Pada kode, tertulis vector yang dimasukan sebanyak 10 buah, sehingga ketika dijalankan browser (saya menggunakan internet explorer 8) akan menampilkan form isian (tiap browser menampilkan bentuk yang berbeda – sepertinya yg paling bagus menurut saya sih Mozilla).
Membuat Inversi matriks 2×2 dan 3×3 dengan Matlab
Aljabar Linear. 18.12.2012. T. Komputer
Berikut ini listing dengan m-file mencari inversi matriks dengan metode operasi baris pada matriks untuk matriks 2×2 dan 3×3. Buka command window dan ketik, misalkan kita ingin memberi nama fungsi tersebut dengan nama fungsi inversi. Ketik kode berikut:
- function y=inversi(x)
- %mencari invers matriks 2×2 dengan
- %operasi baris pada matriks
- %eliminasi gauss
- x=[x eye(2,2)]
- x(2,:)=x(2,:)-((x(2,1)/x(1,1)*x(1,:)));
- x(1,:)=x(1,:)-((x(1,2)/x(2,2)*x(2,:)));
- x(1,:)=x(1,:)/x(1,1);
- x(2,:)=x(2,:)/x(2,2);
- y=[x(:,3) x(:,4)];
>> x=[2 5;6 8]
inversi(x)
x =
2 5 1 0
6 8 0 1
ans =
-0.5714 0.3571
0.4286 -0.1429
Sedangkan untuk matriks 3×3, misalkan kita akan membuat fungsi dengan nama inversi33. Ketik di command window edit inversi33. Ketik kode berikut (sengaja dalam bentuk gambar supaya ngetik sendiri).

Uji di command window dan bandingkan dengan fungsi bawaan Matlab, inv. Bagaimana untuk matriks 4×4 atau yang di atasnya? caranya gampang, gunakan prinsip di atas, atau lihat postingan berikutnya.
Mencari Invers dengan Operasi Baris
Mat. Diskrit. 18.12.2012. Tek. Komputer
Selain dengan Determinan dan Cofactor, mencari invers dapat dilakukan dengan operasi baris pada matriks antara lain:
-
Merubah posisi dua baris dalam suatu matriks
-
Mengalikan seluruh baris dengan suatu konstanta
-
Menambahkan/mengurangkan kelipatan suatu baris terhadap baris lainnya
Berikut ini ilustrasi pengerjaannya dengan contoh suatu matriks:

Sebelumnya, kita hitung dulu determinannya, Det = 22 dan karena tidak sama dengan nol, maka matriks M tersebut memiliki invers. Jejerkan dengan matriks identitas:

Tugas kita adalah melakukan eliminasi gauss agar dihasilkan matriks kiri menjadi matriks identitas. Pertama-tama kalikan baris pertama dengan ½.

Tambahkan tiga kali baris pertama dengan baris kedua sehingga dihasilkan:

Tugas berikutnya adalah membuat elemen baris pertama kolom kedua menjadi nol dengan mengalikan baris kedua dengan 2/11 yang dilanjutkan dengan mengurangi dengan baris pertama sehingga dihasilkan:

Akhirnya, kalikan baris kedua dengan 1/11 agar dihasilkan matriks identitas di bagian kiri:

Setelah matriks sebelah kiri menjadi matriks identitas, maka Matrks inversnya adalah yang di sebelah kanan yakni:

Berikut ini cara mengerjakan dengan Aplikasi Matlab:
>> M=[2 4;-3 5];
>> M=[M eye(2,2)]
M =
2 4 1 0
-3 5 0 1
>> M(1,:)=M(1,:)*1/2
M =
1.0000 2.0000 0.5000 0
-3.0000 5.0000 0 1.0000
>> M(2,:)=3*M(1,:)+M(2,:)
M =
1.0000 2.0000 0.5000 0
0 11.0000 1.5000 1.0000
>> M(2,:)=M(2,:)*1/11
M =
1.0000 2.0000 0.5000 0
0 1.0000 0.1364 0.0909
>> M(1,:)=M(1,:)-2*M(2,:)
M =
1.0000 0 0.2273 -0.1818
0 1.0000 0.1364 0.0909
>> InvM=[M(:,3) M(:,4)]
InvM =
0.2273 -0.1818
0.1364 0.0909
Sumber: Krantz(2009) “Descrete Mathematic Demystified”
Metode Elemen Hingga pada Beam dengan Matlab
Metode Elemen Hingga. 17.12.2012. Teknik Mesin S1
Minggu lalu materi batang thurst telah berakhir dan sekarang kita masuk ke materi beam. Beam berbeda dengan thrust dalam hal gaya yang bekerja. Pada beam, gaya yang bekerja biasanya momen dan bending seperti pada jembatan, jalan, lantai, dan sejenisnya. Beberapa teori mengenai hal ini banyak dijumpai seperti metode defleksi, thimosenko, dan sebagainya.
Berikut ini diberikan contoh kasus, Diketahui A = 2 in, E = 3000000 psi, dan L = 10 cm.
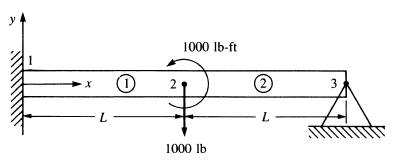
Batang mengalami puntiran dan gaya tekan ke bawah antara elemen (1) dan elemen (2). Ujung kiri dan kanan tidak boleh bergerak (dijepit) dalam arah vertikal. Kita gunakan persamaan yang telah dijabarkan oleh Logan (2007):
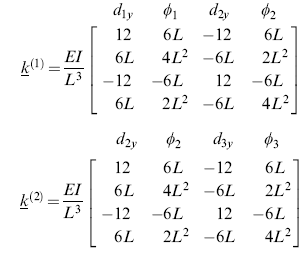 (1)
(1)
Untuk elemen (1) dan elemen (2). Karena koordinat sudah tepat pada x dan y maka tidak perlu melakukan konversi koordinat lagi (tidak perlu tana ^ di atas koordinat). Setelah matriks kekakuan global ditentukan, hubungan gaya luar dengan pergeseran elemen (sudut dan jarak) dapat diketahui.
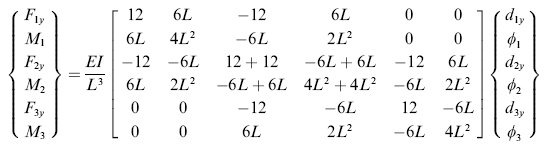 (2)
(2)
Perhatikan kasus di atas untuk mengisi kondisi batas yang ada. Pemahaman kondisi batas sangat penting dalam menyelesaikan kasus yang dihadapi, minimal mengurangi variabel-variabel yang tidak terlibat. Berikut ini adalah kondisi batas yang diidentifikasi:
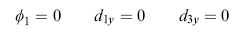 (3)
(3)
Akibatnya adalah persamaan (2) menjadi jauh lebih sederhana:
 (4)
(4)
Buka Matlab, masukan variabel-variabel yang diketahui, E, I dan L serta gaya aksi F. Cari dengan instruksi d=inv(K)*F yang akan diperoleh pergeseran sudut dan jarak di elemen 2 dan 3.
>> A=2;
>> E=3000000;
>> I=500;
>> L=0.1;
>> K=[24 0 6*L;0 8*L*L 2*L*L; 6*L 2*L*L 4*L*L];
>> K2=(E*I/(L^3))*K;
>> F=[-1000;1000;0];
>> d=inv(K)*F
d =
1.0e+004 *
0.0240
1.5312
-1.1250
Konversi Variabel z menjadi z^-1 Pada Sistem Kendali Digital dengan Matlab
Peng. Pengaturan II. 17.12.2012. Teknik Komputer
Ketika kita berbicara sistem kendali digital, beberapa pakar digital yang biasanya berkecimpung dalam bidang Digital Signal Processing (DSP) cenderung menulis fungsi transfer:
 (1)
(1)
Dengan persamaan:
 (2)
(2)
Perhatikan pula, notasi g yang sering digunakan pada sistem kendali kontinue diganti dengan h. Buka Matlab dan buat persamaan (1) dengan kode:

Perhatikan, matlab akan otomatis merubah ke variabel diskrit z karena adanya time sampling sebesar 0.1 di akhir kode. Untuk membentuk menjadi persamaan standar (2), gunakan kode berikut:
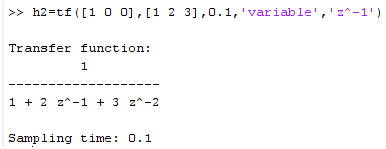
Dengan menambahkan ‘variable’,’z^-1′ di akhir kode. Namun ada sedikit permasalahan untuk kasus fungsi alih sederhana, misalnya h=1/(z+1) karena jika digunakan kode berikut untuk mendapatkan fungsi dengan variabel standar z^-1 diperoleh:

Padahal, prinsip dasarnya adalah mengalikan pembilang dan penyebut dengan pangkat z terbesar yaitu z. Seharusnya pembilangnya berharga 1/z atau z^-1, bukan 1. Oleh karena itu kita harus memodifikasi sedikit persamaan di atas menjadi:

Dengan menambah 0 dibagian pembilangnya agar diperolah hasil yang tepat. Penambahan 0 ini juga tidak berpengaruh terhadap fungsi asalnya. Di sini versi yang digunakan adalah Matlab 2008, mungkin berbeda untuk Matlab 2012.
Menghitung Determinan dan Invers Matriks 4×4
Aljabar Linear. 11.12.2012. T. Komputer
Untuk matriks di atas 3 sepertinya ada kesulitan untuk menghitungny secara manual, beberapa software seperti Matlab, Scilab, dan sejenisnya sudah menyediakan fungsi untuk menghitung determinan dan invers Matriks.

Cara paling mudah adalah dengan metode Sarrus
Determinan berdasarkan gambar di atas:

Sedangkan Matriks Inversnya:

Dengan b11 hingga b44 diperoleh dari perhitungan:

Kalau menurut Anda repot, gunakan saja metode operasi baris dan kolom seperti pada postingan saya berikutnya. Selamat mencoba !
Note: Ada yang nanya masalah adjoint, berikut untuk yg b11, yg lainnya coba sendiri ya … Sorry .. selanjutnya ditranspose, thanks ASD udah ngingetin

NB: Ada saran dari komentar di bawah untuk menggunakan Dodgson Condensation Method yang lebih praktis untuk matriks lebih besar atau sama dengan 3×3
Sumber: http://www.cg.info.hiroshima-cu.ac.jp/~miyazaki/knowledge/teche23.html
Kurva Tegangan – Regangan dengan Excel
Komputer I. 11.12.2012. Tek. Mesin S1
Grafik merupakan representasi data agar lebih mudah dipahami secara visual. Dalam Excel dapat dibuat dengan menekan Insert – Chart.
Tambahkan gambar panah dan text untuk penjelasan terhadap grafik. Untuk panah dengan Shape, sedangkan untuk text dengan Text Box. Daerah elastic merupakan daerah dimana bahan tidak mengalami penambahan panjang.
Buat persamaan yang menhitung nilai regangan akhir setelah tegangan dilepas pada baja tersebut di daerah plastis. Masukan rumus: =IF(A6<9,0,(A6-9)/2)
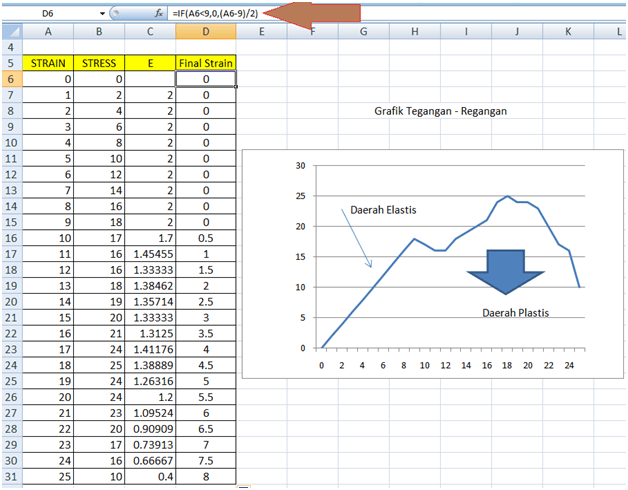
Sebagai contoh, jika pada daerah plastis terjadi regangan 20, maka setelah tegangan dilepas terjadi regangan sebesar 5.5. Jika panjang awal = 5 cm, maka pertambahan panjangnya 5.5 x 5 =27.5
Transformasi Vektor
Metode Elemen Hingga. 09.12.2012. Teknik Mesin S1.
Pertemuan-pertemuan yang lalu telah dibahas metode elemen hingga pada pegas, thrust, heat transfer, dan fluida. Kali ini kita akan membahas konversi koordinat berbagai elemen karena sering dijumpai kita harus merubah koordinat-koordinat yang ada. Misalnya pada kasus batang thrust yang bergeser membentuk sudut alpha dari bidang normal.

Pada gambar di atas, koordinat baru berotasi sebesar tetha. Karena vektor yang baru terbentuk memiliki besar yang sama dengan sebelumnya hanya ada translasi saja, berlaku hubungan berikut ini:
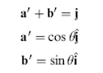
Maka matriks defleksi yang baru (dx).
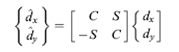
Dengan C dan S berturut-turut Cos ᶿ dan Sin ᶿ. Misalnya kita memiliki kasus di bawah ini diketahui d2x dan d2y berturut-turut 0.1 dan 0.2 in.

Dimana K yang baru adalah:
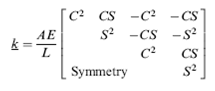
Sebagai contoh sistem di bawah ini:
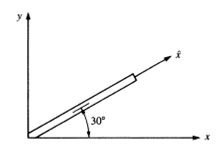
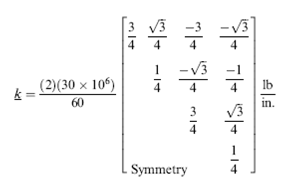
Jika E sebesar 30×106 psi dengan nilai k sebesar:
Membuat Invers Matriks 2×2 dan 3×3 dengan Borland C++
Invers Matriks. 6.12.2012. T. komputer
Setelah determinan dihitung, berikutnya kita coba membuat kode mencari invers matriks tersebut. Perhatikan algoritma pembuatan invers dari pertemuan yang lalu. Lihat kode program di bawah ini.
- #include<stdio.h>
- #include<iostream.h>
- void main(){
- double A[2][2]={1,2,3,4};
- int i,j;
- double det;
-
cout<<“Matriks A = “<<“\n”;
- for(i=0;i<2;i++)
-
{
- for(j=0;j<2;j++)
-
{
- cout<<A[i][j]<<” “;
- }
- cout<<“\n”;
- }
- cout<<“\n”;
- det=A[0][0]*A[1][1]-A[1][0]*A[0][1];
- cout<<“determinan A = “;
- cout<<det;
- cout<<“\n”;
- double A2[2][2];
- A2[1][1]=A[0][0];
- A2[0][0]=A[1][1];
- A2[0][1]=A[0][1]*-1;
- A2[1][0]=A[1][0]*-1;
-
cout<<“Invers A = “<<“\n”;
- for(i=0;i<2;i++)
-
{
- for(j=0;j<2;j++)
-
{
- cout<<A2[i][j]/det<<” “;
- }
- cout<<“\n”;
- }
- }
Jalankan hingga dihasilkan tampilan sebagai berikut:

Untuk matriks 3×3, dengan cara manual dapat dibuat dengan kode berikut ini. Dikatakan manual karena seharusnya kita menggunakan kode yang dapat diterapkan untuk matriks nxn.
- #include<stdio.h>
- #include<iostream.h>
- void main(){
- double A[3][3]={1,2,3,4,5,6,7,8,100};
- int i,j;
- double det;
- double a,b,c;
-
cout<<“Matriks A = “<<“\n”;
- for(i=0;i<3;i++)
-
{
- for(j=0;j<3;j++)
-
{
- cout<<A[i][j]<<” “;
- }
- cout<<“\n”;
- }
- cout<<“\n”;
- //menghitung determinan
- a=A[0][0];
- b=A[0][1];
- c=A[0][2];
- double C1,C2,C3;
- C1=A[1][1]*A[2][2]-A[1][2]*A[2][1];
- C2=(A[1][0]*A[2][2]-A[2][0]*A[1][2])*-1;
- C3=A[1][0]*A[2][1]-A[2][0]*A[1][1];
- cout<<“C1=”<<” “<<C1<<“\n”;
- cout<<“C2=”<<” “<<C2<<“\n”;
- cout<<“C3=”<<” “<<C3<<“\n”;
- det=a*C1+b*C2+c*C3;
- cout<<“Determinan A = “<<” “;
- cout<<det;
- }
Jika dijalankan menghasilkan keluaran:

Uji dengan Matlab apakah jawabannya sesuai:

Cloud Computing Aplikasi Word, Excel, dan Power Point
Komputer I. 05.12.2012. Tek Elektronika
Cloud Computing adalah penggunaan suatu fasilitas (servis) milik orang lain (vendor) yang menyediakan layanan tersebut. Misalnya jika kita ingin mengetik seperti di microsoft word, membuat spreadsheet seperti excel atau membuat power point maka kita dapat menggunakan layanan dari penyedia cloud seperti http://docs.google.com.
Selain menyediakan layanan yang dikenal dengan istilah Software As a Service (SaaS) dikenal juga layanan lainnya seperti storage, platform (operating system), infrastructur (client-server), dan sebagainya. Seperti biasa, Anda diminta login terlebih dahulu (gmail) ke situs tersebut.
Jadi jangan khawatir Anda tidak memiliki fasilitas Word, Excel, dan power point, karena dapat memanfaatkan fasilitas gratis tersebut.
Metode Elemen Hingga Pada Fluida
Fluida secara matematis bisa didekatkan dengan batang thrust, pegas ataupun perpindahan panas. Berikut ini adalah contoh kasus pada batang yang dialiri fluida dengan dua titik 1 dan 2.
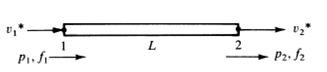
Dengan f, A, K, L, dan p berturut-turut debit, luas penampang, permeabilitas, panjang dan potensial, diperoleh hubungan berikut ini:
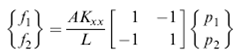
Dengan matriks kekakuannya sebesar:
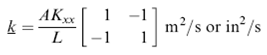
Berikut ini contoh kasus yang akan kita kerjakan dengan bantuan aplikasi Matlab.
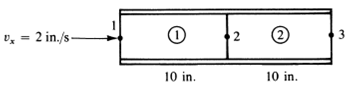
Luas penampang, A = 1 in2. Tentukan kecepatan aliran di titik 2 dan titik 3 jika diketahui kecepatan aliran di titik 1 = 2 in/s. Jawab: Karena bentuknya seragam, matriks kekakuan elemen:
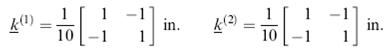
Yang menghasilkan bentuk persamaan umumnya:
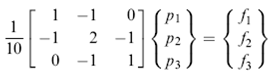
Dari soal diketahui debit f1=v1A=2×1=2 in3/s. Pada elemen (1)
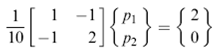
Masukan di Matlab instruksi berikut ini:
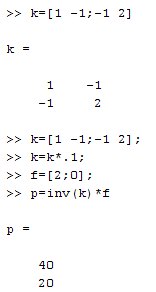
Sehingga diperoleh tekanan di titik 2 sebesar. Untuk mencari nilai kecepatan di titik 2 dan 3 gunakan hubungan: