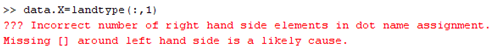Global Variable in Matlab

I still learn Matlab code, and always finding some problems related to script creation. This time I want to share about what in Matlab called “global variable”. This kind of variable at the first time did not attractive to me because I did not find the usefulness of it. Now I understand the important of understanding the global variable.

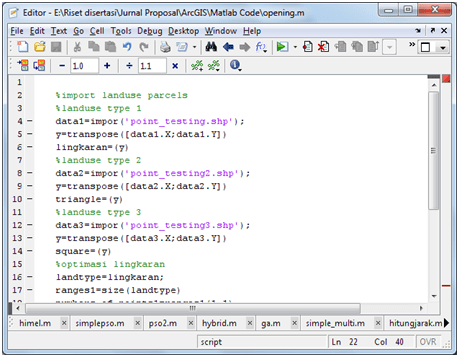
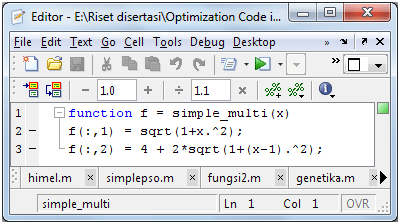
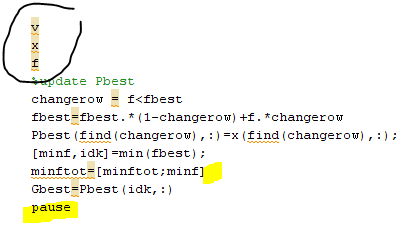
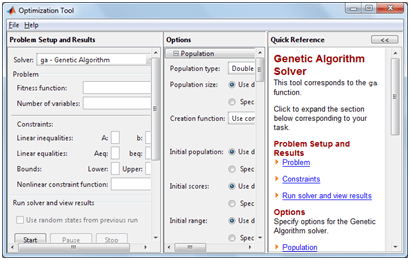
I have created some algorithms such as genetic algorithms for my dissertation. When I try to create the function having many variables, I always been annoyed with an error “undefined variable …” and I revised the code with that variable included. But the declaration seems strange to me, like this.

So, I try to solve that problem by searching in the internet. I found that I have to use global variable that used everytime when some function called the variable. Explanation in web officially from mathworks is here. For everyone who like video in youtube, this problem is explained clearly here. Now I try to fix my function using global variables, and I do not have to delcare many variables in my function.

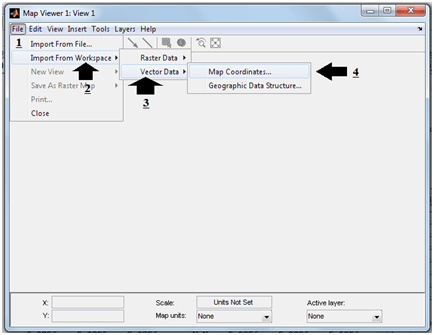
Let’s we try some simple function. We have to create main function and other function to calculate something from main function. For example we name the main function “energy” that called other function to calculate the internal energy “calc”. Type in the command window >> edit calc to create calc.m function. The message will be opened:

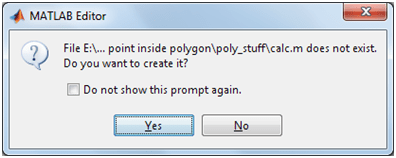
Just click “Yes” because it only informed that calc.m does not exist. But becarefull if the message does not shows to us. It means the name of our function has been used in Matlab, so we have to change to other names.

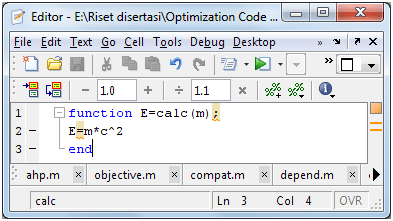
Now in the same way, create new m-file for main function with the name e.g “main”. Make sure your m-file name is not Matlab built-in functions.

Now try to run the m-file by clicking the run icon (green triangle). There is an error message:

You have to include the variable c in your calc function or you have to declare that variable in your main file as global variable. Add c as our global variable in the main function. Revise your main and calc file to include global variable c:

And try to run again, you have to get the result without error message (don’t forget to save your m-file everytime you edit it). No need to include c in calc variable function anymore 🙂.

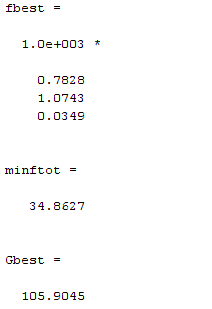
E =
1.8000e+018
ans =
1.8000e+018

NOTE: future of Matlab said that … Ok, I paste the warning:

Warning: The value of local variables may have been changed to match the
globals. Future versions of MATLAB will require that you
declare
a variable to be global before you use that variable.

So, we have to declare global c first before declare c=300000000;

Mengidentifikasi Pola Citra dengan Jaringan Syaraf Tiruan

Sebelum membahas identifikasi perlu diketahui ada dua jenis pengecekan suatu citra yaitu identitikasi (identification) dan pencocokan (verification). Pada sistem pencocokan prinsipnya sama dengan mengecek password, misalnya mengecek tanda tangan, sistem akan membandingkan identitas orang yang malakukan tanda tangan dengan citra tanda tangannya. Mirip ketika mau log-in, kita memasukan user id dan kemudian password, tetapi di sini passwordnya diganti dengan sidik jari, tanda tangan, retina, dll. Tetapi sistem identifikasi sedikit lebih rumit karena sistem tidak diberitahu identitas yang melakukan biometrik. Sistem harus mengetahui siapa pemilik citra yang ditangkap sistem. Jadi ketika kita ingin memasuki gedung yang diberi pengaman sistem identifikasi, pengguna hanya memberikan sidik jari, retina, tanda tangan, dan biometrik lainnya yang biasanya non-destruktif (kalo kesetrum mungkin sedang sial aja .. he he).

Untuk identifikasi tanda tangan dibutuhkan pengolahan citra sebelum masuk ke sistem identifikasi. Untuk belajar sebaiknya kita coba sistem yang sederhana misalnya membedakan angka 1,2, dan 3 saja dan tanpa pengolahan citra, alias kita beri tahu langsung vektornya. Gambar berikut ini menunjukan angka 1, 2, dan 3 di pixel berukuran 5×3.

Angka satu di sini menunjukan adanya pola sementara nol tidak. Data tersebut data utama yang akan ditraining dengan Jaringan Syaraf Tiruan (JST). Tentu saja jika hanya data itu yang diberikan, hasilnya kurang bagus karena sistem membutuhkan data lain untuk menjaga masukan yang agak menyimpang misalnya gambar di bawah untuk angka 1.

Untuk angka-angka yang lain, coba buat sendiri deviasinya. Kalo tanda tangan, untuk training user diminta melakukan beberapa tanda tangan, karena kebetulan hampir tidak mungkin melakukan tanda tangan beberapa kali hasilnya sama persis.

Langkah pertama adalah membuat vektor tanda tangan, caranya adalah mengkonversi matriks tanda tangan menjadi vektor dengan fungsi reshape di Matlab. Buka command window, kita coba untuk angka satu terlebih dahulu.

>> satu=[0 1 0;0 1 0;0 1 0;0 1 0;0 1 0]
satu =
0 1 0
0 1 0
0 1 0
0 1 0
0 1 0
>> satu=reshape(satu,1,15)
satu =
Columns 1 through 12
0 0 0 0 0 1 1 1 1 1 0 0
Columns 13 through 15
0 0 0

Perhatikan fungsi reshape di atas, matriks 5×3 diubah menjadi 1×15 dimana 15 dari perkalian 3×5 (masukan angka 3, kali dan angka 5 di calculator iphone 6 Anda, nanti keluar deh angka 15 .. he he). Lakukan untuk tiga deviasi dari angka satu di gambar atas. Lakukan juga hal yang sama untuk angka 2 dan angka 3. Bagaimana jika tanpa deviasi? Ya bisa saja, tapi yang namanya belajar/training membedakan monyet dengan bukan monyet aja ga bisa kan trainingnya dengan gambar monyet saja, harus dengan gambar yang lain, bisa dengan foto teman anda, atau foto anda juga boleh. Ok, kita beri label saja monyet, eh angka satu, dua, dan tiga berturut-turut 1,2,3 walau boleh saja 0, 10, 20. Tetapi supaya gampang mengenali yang pertama saja. Supaya cepat, ok 2 dan 3 untuk training tidak perlu deviasi. Angka satu dengan tiga deviasi. Secara prinsipnya adalah gambar berikut:

Kolom terakhir merupakan label/target, sementara vector1 sampai 3 berukuran 1×15. Buka lagi command window, lakukan cara yang sama dengan variabel satu di atas, beri nama saja berikutnya dengan satua, satub, satuc, dua, dan tiga.

>> satua=reshape(satua,1,15);
>> satub=reshape(satub,1,15);
>> satuc=[0 0 1;0 0 1;0 1 0;0 1 0;0 1 0];
>> dua=[1 1 1;0 0 1;1 1 1;1 0 0;1 1 1];
>> tiga=[1 1 1;0 0 1;0 1 1;0 0 1;1 1 1];
>> satua=reshape(satua,1,15);
>> satub=reshape(satub,1,15);
>> satuc=reshape(satuc,1,15);
>> dua=reshape(dua,1,15);
>> tiga=reshape(tiga,1,15);
>> datalatih=[satu;satua;satub;satuc;dua;tiga];
>> target=[1;1;1;1;2;3];

Latih dengan toolbox JST di Matlab dimana data pelatihannya datalatih dan targetnya target. Format di nntool sedikit berbeda dengan data di atas dimana kolom jadi baris dan baris jadi kolom. Gunakan newdatalatih dan newtarget di toolboxnya.

>> newdatalatih=transpose(datalatih);
>> newtarget=transpose(target);

Oke, kita cek hasilnya yuukk. O iya, kalo masih bingung utak-atik toolbox JST (nntool) bisa dibuka di link sebelumnya, gampang kok. Kita uji dengan angka satu, dua dan tiga.

>> tessatu=transpose(satu);
>> sim(network1,tessatu)
ans =
1.0000
>> tesdua=transpose(dua);
>> sim(network1,tesdua)
ans =
2.0000
>> testiga=transpose(tiga);
>> sim(network1,testiga)
ans =
1.5786
>> tessatua=transpose(satua);
>> sim(network1,tessatua)
ans =
1.0000

Gimana .. ada yang ngaco ga? … ternyata, A D A. Angka tiga dites kok keluarnya 1,58 (saya beri warna merah). Makanya ngajarin bedain monyet atau bukan jangan hanya data monyet saja yang dilatih. Ok, selamat berpusing-pusing ria yang dapat skripsi atau tesis tentang identifikasi tanda tangan ya (jadi inget kerjaan saya dulu) ..

Jika Anda bisa membuat pengolahan citra di bawah ini berarti sudah siap nih untuk sistem identifikasi pola .. Gambar di bawah ini hasil keluaran angka dua (lihat bagian putihnya, karena angka 1 berwarna putih dan angka nol berwarna hitam).

Oiya, kalo bisa gunakan Matlab 7 sepertinya lebih ampuh. Bukan Cuma tanda tangan, bisa juga mengenali grafik lho, lihat di sini.

Writing Genetic Algorithms in Matlab

Genetic Algorithms (GAs) toolbox is available when we install Matlab, but some cases need special treatment to our system. It may be related to constraint, and may be combination to other algorithms. Some students when doing their thesis or project need some manipulations to the algorithms. There are many books give additional source code for GAs. But the main source for me is an internet. We can find a lot of source code in Matlab by using a simple google. For example sivanandam in his book give a code in matlab but there are so many additional script that must be available first in order to make our code running well. One site that may be important to GAs user is here. One simple GAs may be need some m-file scripts like this.

Of course you can just type “optimtool” in command window, and choose GAs as your basis of optimization. But understanding something inside it I think very important, how selection, crossover, etc. so we can manipulate them for giving better efficiency, accuracy and speed.

Creating a Region for Constraint in ArcView

This is an example to create a region drawing from ArcView/ArcGis. Open the ArcView and do these steps:

Because we will draw a region, we will use polygon as a basis of our theme. The window will be appeared everytime we create new theme.

After clicking “OK” you must save and give the name for this new region, e.g “boundaryshp”. Now we start a new boundary polygon as a constraint of our Multiobjective Evolutionary Algorithms (MOEAs). For example we draw the region like figure in dark red color below:

Then we export it to matlab (of course in matlab we say read/impor). Use this script in command window to read the boundary region. But, firstly we have to save.

data=shaperead(‘boundaryshp.shp’)

This will retrieve a shapefile. But we have to mine the coordinates, using:

y=data.Y;
x=data.X;

You can use mapviewer to open that region in Matlab. Import from workspace after mapviewer appear.

You have to select X and Y coordinates. In our example y and x.

If you do not find any problems, your region will appear like this … meauwww !!

So, we’ve just believed that our spatial data was exported to matlab workspace. The last part is convert the spatial data into coordinates according to our requirements. As an information, the shapefile have row-based style, so we have to transpose them.

y=transpose([data.X;data.Y]);
y
y =
1.0e+006 *
0.7192 9.3096
0.7194 9.3096
0.7196 9.3099
0.7199 9.3102
0.7204 9.3103
0.7205 9.3102
0.7202 9.3100
0.7202 9.3099
0.7202 9.3096
0.7199 9.3098
0.7197 9.3095
0.7198 9.3092
0.7197 9.3091
0.7196 9.3094
0.7194 9.3096
0.7193 9.3095
0.7192 9.3096
NaN NaN
0.7192 9.3096
0.7192 9.3096
0.7192 9.3096
0.7192 9.3096
NaN NaN

Note: May be I rather bad in creating some region, there are two NaN that actually only one pair. It must be there are two closed region on that shapefile.

Mencari Pareto Front dengan Kode Matlab

Lanjutan dari postingan terdahulu. Setelah surfing di internet, akhirnya ketemu juga program untuk menentukan titik pareto front di titik-titik hasil optimisasi di situs ini. Kode-nya dibuat oleh Yi Cao dari Cranfield University pada tahun 2007 yang lalu. Sayangnya gabungan hex file dengan m-file. Letakan dalam satu folder setelah diekstrak, dan jalankan kode ini di command window:

X = rand(100,2);
front = paretofront(X);
hold on;
plot(X(:,1),X(:,2),’.’);
plot(X(front, 1) , X(front, 2) , ‘r.’);
hold off
grid on
xlabel(‘X_1’);
ylabel(‘X_2’);
title(‘Pareto Front of a set of random points’);

Prinsipnya adalah, fungsi paretofront akan mencari titik-titik pareto dimana tidak ada titik lain yang kedua fungsi objektif lebih kecil dari titik tersebut (kalau hanya satu masih diperbolehkan). Pada grafik, titik-titik yang merupakan pareto front diplot berwarna merah.

Note: Untuk mencari optimasi maximum tinggal mengalikan X dengan -1 di fungsi paretofront

front = paretofront(X*-1);

Simple Pareto Front dengan Matlab (Multiobjective)

Kalau dulu multi objective diselesaikan dengan memberi bobot terhadap tiap-tiap fungsi objektif atau dengan hierarki, saat ini teknik tersebut mulai ditinggalkan dan diganti dengan non-dominate objectif atau dikenal dengan istilah pareto, yang diusulkan pertama kali oleh pareto pada tahun 1896. Jadi kita tidak memaksakan memberi bobot terhadap fungsi-fungsi objektif dan memberikan range tertentu terhadap hasil optimasi. Range tersebut makin luas makin baik (wide spread). Misalnya penjelasan yang dapat dilihat di situs ini, kita coba jalankan dengan Matlab.

Ada dua fungsi objektif yang akan dicari nilai optimalnya (biasanya nilai minimum). Perhatikan dua grafik ini yang memiliki dua nilai minimum tergantung fungsi mana yang digunakan.

Untuk melakukan optimasi terhadap dua objektif fungsi di atas (fungsi garis merah dan garis biru). Sebelumnya buka matlab editor untuk membuat satu fungsi baru dengan mengetik di command window:

>>edit simple_multiobjective

Ternyata Matlab sudah membuatkan fungsi tersebut, sepertinya untuk demonstrasi optimasi multiobjektif. Untuk mengoptimasinya, fungsi yang digunakan di Matlab adalah gamultiobj. Ketik atau copas kode ini ke command window:

FitnessFunction = @simple_multiobjective;
numberOfVariables = 1;
[x,fval] = gamultiobj(FitnessFunction,numberOfVariables);

Di sini disebutkan jumlah variabel 1, yaitu x saja. Kemudian di sebelah kiri sama dengan ada x dan fval sebagai hasil dari optimasinya. Untuk melihat isinya dapat kita ketik di command window x dan fval tersebut. Apa hasilnya?

Hasilnya adalah matlab memberikan beberapa hasil optimasi (berupa range) kombinasi dari cenderung optimal di fungsi satu hingga ke optimal di fungsi dua. Ketik di command window untuk melihat grafiknya:

>> plot(fval(:,1),fval(:,2),’*’)

Hasilnya berupa grafik pareto dari nilai optimal dua fungsi tersebut. Di sini bobot bervariasi dari kecenderungan ke fval pertama hingga ke fval kedua. Fval adalah nilai optimal fungsi-fungsi fitness nya.

Bagaimana jika tiga fungsi objektif? Tentu saja kalau ingin divisualisasikan nanti berupa grafik tiga dimensi. Bagaimana jika empat objektif? Seperti disertasi saya, tentu saja sulit digambarkan. Matlab juga menyediakan visualisasi yang bagus (running ketika program berjalan) dengan memasukan kode di command windows sebagai berikut:

A = []; b = [];
Aeq = []; beq = [];
lb = -1.5;
ub = 0;
x = gamultiobj(FitnessFunction,numberOfVariables,A,b,Aeq,beq,lb,ub);
options = gaoptimset(‘PlotFcns’,{@gaplotpareto,@gaplotscorediversity});
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);

Bikin Buku Lagi .. “Pemrograman Database dengan Matlab”

Menganggur saat bulan puasa ternyata enak juga buat menulis. Saat berada di “dunia” sendiri tiba-tiba adzan maghrib pertanda waktu berbuka puasa. Setelah berbuka, refresh lagi, dan siap meracik tulisan lagi. Setelah lebaran, jadilah satu buku “Pemrograman Basis Data dengan Matlab”. Belum tentu itu judulnya karena terkadang penerbit menyarankan untuk mengganti judul dengan judul yang menarik dari sisi pemasaran. Begitulah, harus terjadi kerjasama yang baik antara penulis dengan pemasaran, jika tidak, sudah dapat dipastikan buku tersebut tidak laku.

Sebenarnya buku yang sedang direview oleh penerbit (semoga lolos) tersebut berawal dari pertanyaan-pertanyaan di blog ini. Lalu muncul ide bagaimana jika dibuat dalam satu paket buku beserta contoh-contoh aplikasinya. Apalagi banyak yang masih sangsi bahwa Matlab bisa menghasilkan aplikasi yang terhubung dengan basis data seperti bahasa-bahasa yang lain seperti visual basic, java, dan bahasa pemrograman visual lainnya. Matlab selama ini dipuji karena tangguh di sisi komputasi. Bukan tangguh sih sebenarnya, tetapi mudah dan user friendly. Jadi jika bisa mengelola database, maka perancang bisa dengan baik menghubungkan komputasi teknis, soft computing, data mining, dengan basis data yang dimiliki. Database Management System (DBMS) yang dipilih adalah Microsoft Access sebagai perwakilan DBMS desktop dan MySQL untuk DBMS berbasis web. Sepertinya cukup karena keduanya merupakan DBMS yang paling banyak digunakan saat ini, terutama mahasiswa.

Untuk contoh aplikasi, dipilih kasus-kasus yang sering dijadikan tugas akhir (skripsi atau thessis) para mahasiswa yaitu data mining dengan clustering, enkripsi database, pengolahan citra, yang dirakit tentu saja dengan GUI. Tulisan diakhiri dengan lampiran-lampiran yaitu pembuatan executable program dan teori dasar struktur data di Matlab yang sangat penting karena proses perpindahan dari DBMS ke Matlab untuk diproses dan sebaliknya.

Seperti biasa, operasi dasar pada pemrograman basis data dipelajari yang dikenal dengan istilah CRUID (create, read, update, insert, dan delete). Pembuatan grafik setelah proses clustering dan pengolahan citra digital yang kemudian disimpan ke database dibahas dengan sederhana. Jika tombol “clustering” ditekan maka tiap record di database data langsung terupdate masuk kluster yang mana (kluster 0 atau 1). Tentu saja Anda bisa mengembangkan menjadi lebih dari dua kluster. Tanda tangan yang tadinya image kini dirubah menjadi biner (0 dan 1) yang bermanfaat untuk mengurangi kapasitas penyimpanan (dibandingkan penyimpanan dalam bentuk image utuh) yang biasanya diterapkan di perbankan.

Sepertinya pengolahan data dengan notepad atau excel yang bersifat offline dari database sudah mulai diganti dengan sistem yang online karena perubahan data terjadi secara cepat dengan jumlah yang besar (big data). Semoga buku seharga beberapa bungkus rokok tersebut segera terbit (whee lah …). Amiin.

Menentukan Suatu Titik di Dalam atau di Luar Polygon

Setelah berhasil merancang algoritma yang berfungsi mengoptimasi beberapa lokasi landuse, berikutnya adalah merancang optimasi dengan batasan. Tidak ada gunanya merancang sistem yang mengoptimasi lokasi optimal tetapi tidak melibatkan batasan tertentu. Batasan di sini misalnya lokasi yang menjadi target lokasi optimal harus bebas banjir, tidak berbahaya, dan aspek-aspek suitability/kesesuaian sesuai jenis peruntukan lahannya (perumahan, kantor, komersial, dan lain-lain). Dengan demikian saat proses optimasi, harus terlebih dahulu dipastikan bahwa kandidat lokasi tersebut berada di dalam region yang diperbolehkan. Istilah untuk optimasi jenis ini adalah constraint optimization.

Ilmu yang mempelajari apakah satu titik berada di dalam dan di luar suatu polygon adalah computer graphic. Secara gampangnya, suatu titik berada di dalam suatu area apabila beririsan dengan garis/lengkungan area tersebut tepat satu kali, dimana garis itu ditarik dari titik yang akan diuji pada sumbu x atau sumbu y keluar/menjauh. Jika beririsan dua kali, atau tidak sama sekali, maka dipastikan titik tersebut berada di luar bidang area tersebut. Cukup sederhana tetapi prakteknya sangat sulit. Setelah searching di internet, ternyata sudah banyak yang membuat M-file dengan bahasa Matlab, salah satunya adalah pada link berikut ini.

Karena Area of Interest (AOI) riset saya adalah kota Bekasi, maka saya membutuhkan region kota Bekasi dalam format shapefile (*.shp). Data dapat diunduh (biasanya berupa data untuk seluruh kota di Indonesia). Lakukan proses clipping untuk menemukan region kota Bekasi saja. Setelah itu impor ke dalam workspace dengan instruksi:

data1=impor(‘bekasi_city.shp’);
y=transpose([data1.X;data1.Y]);
land=(y);

Fungsi impor saya buat sendiri, untuk mempermudah saja, yaitu fungsi shaperead, yang bisa Anda lihat dengan mengetik ‘help shaperead’ di command window untuk lebih jelasnya. Untuk melihat secara visual regionnya, gunakan ‘mapview’ dan buka file shapefile yang Anda miliki.

Letakkan kursor di dalam region kota Bekasi, catat koordinatnya, kemudian cek apakah berada di dalam kota Bekasi atau di luar kota Bekasi. Misalnya titik yang berada di dalam adalah (106.98, -6.27), ikuti instruksi berikut ini untuk mengecek apakah berada di dalam atau di luar.

p1=[106.98 -6.27]
p1 =
106.9800 -6.2700
>> in=inpoly(p1,land)
in =
1

Perhatikan, Matlab menjawab 1, yang berarti titik berada di dalam kota Bekasi. Bagaimana jika di luar kota Bekasi? Arahkan mouse di luar kota Bekasi, catat koordinatnya, misalnya (107, -6), test lagi:

p=[107 -6];
in=inpoly(p,land)
in =
0

Matlab menjawab nol, yang artinya di luar region/area. Jadi kode teruji benar. Terjawablah sudah problem menentukan suatu titik di luar atau di dalam region yang nantinya akan diintegrasikan dengan algoritma optimisasi. Akhir kata, fungsi di atas juga bisa digunakan untuk deretan titik, tidak harus satu titik saja. Misalnya kedua titik di atas, titip pertama p dan titik kedua p1, akan dicek secara bersama, kita tinggal menggabungkan kedua titik tersebut menjadi variabel titik:

test = [p;p1]
test =
107.0000 -6.0000
106.9800 -6.2700
in=inpoly(test,land)
in =
0
1

Yang artinya titik pertama di luar dan titik kedua didalam. Selamat mencoba dan bermain-main dengan data spatial dengan Matlab.

Koneksi Matlab dengan ArcGIS/ArcView

Sempet juga saya kelabakan ketika menerima hibah penelitian tentang spatial data yang diintegrasikan dengan algoritma tertentu. Karena kepepet, waktu itu saya menggunakan GUI matlab untuk membuat peta seperti arcgis dan juga bantuan aplikasi google map/earth yang ditempel di web berbasis ruby on rails, karena waktu kuliah web technology saya diajarkan bahasa pemrograman ruby on rails. Hasilnya kira-kira berikut ini:

Meneruskan riset yang sederhana tentang optimasi lokasi, untuk optimasi landuse tentu saja tidak bisa dengan cara seperti optimasi spbu yang memang terletak di pinggir jalan. Landuse akan mencari areal dua dimensi yang luas sekali, terutama untuk kasus kota bekasi yang luasnya sekitar 200 km persegi. Ternyata rumit juga terutama criteria/objective function untuk suitability. Ditambah lagi constraint untuk candidate locations, weh. Untuk sementara hasilnya seperti ini, semoga lancar ke depannya.

Optimasi Landuse dengan Matlab

Saatnya mulai membuat kode program matlab untuk mengoptimasi lokasi landuse dan landcover dengan data dari arcview/arcgis. Banyak algoritma yang digunakan oleh riset-riset optimasi saat ini, dua yang terkenal yaitu dengan Particle Swarm Optimization (PSO) dan Genetic Algorithms (GAs). Karena masing-masing memiliki kelemahan dan kelebihan, banyak yang berusaha melakukan hybrid antara satu metode dengan metode lainnya yang ternyata menghasilkan efisiensi dan akurasi yang baik.

Gambar di atas memperlihatkan hasil optimasi landuse tipe lingkaran. Di sini kode masih agak error, dan belum menerapkan algoritma untuk constraint (terlihat result berwarna hijau kabur melewati batas wilayah), tapi untuk sementara cukup menggembirakan karena dapat menghubungkan antara matlab dengan arcview/arcgis untuk menampilkannya. Setiap selesai melakukan optimasi, untuk melihat hasilnya kita harus merefresh Arcview dengan menekan tombol layer .

Menjawab Problem Data type “Struct” di Matlab

Menjawab permasalahan yang dijumpai ketika membuat kode program dengan bahasa Matlab adalah dengan cara: 1) membaca help, 2) situs www.matworks.com, 3) komunitas di internet, dengan bantuan google, dan 4) youtube. Permasalahan muncul karena karakter bahasa matlab yang sedikit berbasis objek. Buku yang beredar di pasaran pun tidak sanggup menjawab seluruh pertanyaan yang beredar. Pertanyaan-pertanyaan liar selalu bermunculan baik melalui komentar ataupun email. Salah satu yang bikin ribet adalah masalah struktur data, karena Matlab memiliki struktur data yang agak banyak. Banyaknya struktur data mungkin dikarenakan kemudahan-kemudahan yang matlab berikan melebihi bahasa induknya yaitu c++ dan fortran.

Beberapa kata kunci yang melibatkan struktur data di matlab dan dapat diakses di fasilitas help antara lain: num2str, cellstr, num2cell, dan sebagainya. Untuk mengetahui tata caranya secara cepat dengan cara mengetik di command window, misalnya: >>help num2str.

Yang menarik di sini, kita dapat mengetahui pula fungsi-fungsi yang berhubungan dengannya lewat informasi “See also”. Untuk mengetahui secara detail dalam bentuk GUI yang rapi dapat mengganti help dengan doc sebelum kata fungsi yang ingin kita ketahui lebih lanjut. Atau menekan tulisan doc num2str.

Untuk situs resmi matlab, sepertinya formatnya tidak jauh berbeda dengan help, yang memaksa kita untuk membaca luas yang terkadang jadi lupa dengan masalah utamanya. Sepertinya andalan utama untuk saat ini adalah searching di internet dengan search engine tercanggih di dunia, google (www.google.com). Untuk bahasa pemrograman, biasanya google mengarahkan ke situs resmi dan komunitas programming, seperti misalnya stackoverflow (www.stackoverflow.com). Perhatikan jawaban di bawahnya oleh para senior, misalnya pertanyaan untuk kasus saya di muka berikut ini:

Terkadang kita tidak mengenal fungsi-fungsi tertentu, karena memang jumlahnya sangat banyak dan tidak mungkin dihapal semuanya. Nah, di sini karena yang ikut terlibat adalah programmer-programmer dengan latar belakang yang beragam, bagi programmer tertentu mungkin banyak memakai fungsi tertentu yang khas di bidangnya yang bagi orang di bidang lain masih dianggap asing. Contoh di atas adalah fungsi setfield yang masih asing bagi pemula atau yang menggunakan matlab untuk komputasi yang tidak berhubungan dengan database. Ikuti di command window saran di atas, dan berhasil. Tentu saja andalan utama kita adalah help yang resmi dari Matlab. Berikut ini trik untuk mengupdate nilai field dari data jenis struct.

Misalkan kita punya data landtype:

landtype =
4134884 7681103
9275435 3020821
2063774 5498421
5850328 1631791
5932021 1324960
4557209 2641519
1531668 5462547
2804685 2757848
7250245 6744421
- ……….

Akan dimasukan ke variabel struktur “data” untuk variabel X dan Y di dalam data tersebut.

data =
17×1 struct array with fields:
Geometry
X
Y
ID

Dengan mengetikan instruksi ini, fields X dan Y akan berisi landtype.

for i=1:17
data(i).X=landtype(i,1)
data(i).Y=landtype(i,2)
end

Kita uji, misalnya untuk data pertama.

>> [data(1).X data(1).Y]
ans =
4134884 7681103

Bernilai sama dengan landtype pada data di atas yang dicetak tebal. Berikutnya akan kita ekspor hasilnya menjadi shapefile agar bisa dibuka di arcview / arcgis.

>> shapewrite(data,’result’)

Pareto Front Optimal

Belajar sesuatu terkadang lebih mudah dengan langsung mempraktekannya. Kata pepatah experience is the best teacher. Matlab menyediakan fasilitas help baik yang terselip di programmnya atau di situs resminya, www.mathworks.com.

Buka matlab, buat fungsi objective yang akan diminimisasi. File – New – Function, atau saya lebih suka langsung mengetik di command window nama M-file yang akan saya buat >>edit simple_multi. Tekan enter ketika Matlab mengkonfirmasi bahwa M-file yang dimaksud tidak ada dan apakah kita akan membuatnya.

Ada dua fungsi di dalam satu fungsi pada M-file di atas. Tugasnya adalah mencari nilai X yang membuat dua fungsi itu minimum. Tidak ditentukan di awal bobot antara fungsi 1 dan fungsi 2 karena kalau bobotnya sudah ditentukan tentu saja langsung bisa ketemu jawabannya. Bobot yang kita gunakan bobot standar yang jika dijumlahkan = 1, misalnya w1=0.3 dan w2=0.7. Ikuti saja instruksi dari www.mathworks.com untuk memperoleh nilai x beserta bobotnya.

F = simple_multi(t);
t = linspace(-0.5,1.5);
plot(t,F, ‘LineWidth’ ,2)
hold on
plot([0,0],[0,8], ‘g–‘ );
plot([1,1],[0,8], ‘g–‘ );
plot([0,1],[1,6], ‘k.’ , ‘MarkerSize’ ,15);
text(-0.25,1.5, ‘Minimum(f_1(x))’ )
text(.75,5.5, ‘Minimum(f_2(x))’ )
hold off
legend( ‘f_1(x)’ , ‘f_2(x)’ )
xlabel({‘x’ ; ‘Tradeoff region between the green lines’ })
edit pickindex
k = 1;
[min1,minfn1] = fminbnd(@(x)pickindex(x,k),-1,2);
k = 2;
[min2,minfn2] = fminbnd(@(x)pickindex(x,k),-1,2);
goal = [minfn1,minfn2];
nf = 2;
N = 50;
onen = 1/N;
x = zeros(N+1,1);
f = zeros(N+1,nf);
fun = @simple_multi;
x0 = 0.5;
for r = 0:N
t = onen*r; % 0 through 1
weight = [t,1-t];
[x(r+1,:),f(r+1,:)] = fgoalattain(fun,x0,goal,weight, …
[],[],[],[],[],[],[]);
End

Grafik pertama berisi grafik dua fungsi objective yang akan dioptimasi:

Kita harus mengkompromikan antara f1 dan f2 karena ketika f1 ke arah minimum, fungsi f2 naik nilainya. Pareto menggunakan prinsip nondominant dimana tidak boleh ada yg dominan antara f1 dan f2. Perhatikan grafik kedua dari instruksi di atas:

Grafik di atas adalah sebaran beberapa komposisi bobot w1 dan w2 terhadap kedua fungsi objective. Titik2 itu membentuk garis lengkungan yang menggambarkan nondominant. Titik terbaiknya dapat dilihat dari panduan di link ini, perhatikan gambarnya.

Particle Swarm Optimization (PSO) – dengan Octave

Tulisan ini merupakan lanjutan dari tulisan sebelumnya yang menggunakan Matlab sebagai medianya. Ketika membuka Octave pertama kali, ada dua pilihan yaitu mode Command Line Interface (CLI) atau Graphical User Interface (GUI). Kita pilih yang mudah saja yaitu GUI. Tampak tampilan yang mirip dengan matlab. Untuk yang ingin menginstallnya, baca postingan saya yang lalu.

Seperti pada Matlab, Octave juga membutuhkan direktori kerja dimana M-file yang telah kita buat berada. Di sini saya harus menempatkan dua file yaitu file algoritma PSO, simplepso.m dan fungsi2.m yang merupakan fungsi tujuan (objective function) yang akan dioptimalkan.

Tampak hasil optimasi untuk 4 iterasi dengan fungsi pause yang saya sisipkan untuk melihat perjalanan program tiap operasi. Di sini sedikit berbeda, ketika Octave menjumpai fungsi pause ternyata ada pesan agar kita menekan huruf f yang artinya forward (maju).

Grafik di atas merupakan hasil plot yang kecanggihannya ga jauh beda dengan Matlab. Harga Octave pun tidak terlalu mahal, hanya Rp. 0,- alias gratis, dibanding harga lisensi Matlab versi stand alonenya (individual price) sekitar Rp. 34 juta dengan harga 1 dollar yang saat ini melambung Rp. 13.000,-.

Particle Swarm Optimization (PSO)

PSO jika diterjemahkan berarti optimasi segerombolan partikel. Partikel di sini adalah makhluk hidup seperti burung, ikan, atau lebah yang sedang mencari makanan. Mengapa mengikuti prinsip pergerakan segerombolah makhluk-makhluk tersebut? Jawabannya sederhana, karena makhluk-makhluk tersebut berhasil menemukan makanannya. PSO pertama kali dicetuskan oleh kennedy dan Eberhart pada tahun 1995 yang membahas mengenai perilaku kerumunan makhluk hidup.

Menurut beberapa paper, misalnya Sathya, yang melakukan optimasi terhadap segmentasi gambar, PSO memiliki beberapa kelebihan di antaranya:

Mudah diimplementasikan dan hanya sedikit parameter yang dibutuhkan.
Tidak ada evolusi pada operatornya, misalnya mutasi dan crossover pada Genetic Algorithms (GAs).
Di GAs kromosom membagi informasi sehingga pergerakan mengikuti group-nya sendiri, berbeda dengan PSO yang berkelompak, dan menurut Sathya PSO lebih robust. Sepertinya saya kurang setuju dengan pendapat yang ini, apa boleh buat kita rujuk saja.
PSO lebih efisien karena membutuhkan sedikit komputasi.
Dibanding GAs dan metode heuristik lainnya, PSO lebih fleksibel dalam menjaga keseimbangan antara pencarian global dan lokal terhadap search space-nya.

Salah satu point menarik yang dibahas oleh kennedi et al. adalah masalah collision karena jika setiap partikel menganggap ada partikel lain yang lebih “optimum” tentu saja dia akan mengarah ke sana dan terjadi tuburukan/collision. Tetapi kenyataannya tidak ada tabrakan saat burung terbang, ikan berenang, lebah menari-nari dan sebagainya.

Untuk menerapkan algoritma PSO, di sini kita coba dengan menggunakan matlab atau octave. Kita coba terlebih dahulu dengan matlab. Sebagai referensi, Anda dapat mendownload materi budi santoso dari ITS di link berikut, kemudian coba jalankan kode yang ada di dalamnya. Di sana dijelaskan dua jenis PSO dengan dan tanpa inersia. Agar lebih mudah memahami alur instruksi programnya, di bawah instruksi yang akan saya selidiki biasanya saya sisipkan instruksi pause dan titik kemo di belakang kode yang dibuat saya hilangkan titik koma-nya agar muncul di layar command window. Saya coba jalankan dengan jumlah partikel 3 dan iterasi maksimum 4.

Variabel v,x,f yang menyatakan nilai awal kecepatan, swarm, dan nilai fitness-nya dimunculkan dalam variabel yang saya lingkari di atas. Untuk menampilkan nilai minimum minftot saya hapus titik komanya agar muncul di command window ketika berhenti sejenak di tiap iterasi karena instruksi pause yang saya sisipkan. Hasilnya tampak di bawah ini dimana fitness yang terbaik adalah pada swarm ketiga (34.8627) dengan swarm 105.9045. Ini tentu saja masih belum optimal karena masih iterasi pertama.

Setelah iterasi keempat dijalankan dengan menekan sembarang tombol untuk melanjutkan akibat instruksi pause tersebut diperoleh grafik dan hasil akhir. Kita coba dengan octave, di tulisan selanjutnya

Octave – Matlab Versi Gratis

Lanjutan postingan sebelumnya yang kurang memuaskan nih, kita coba selain scilab. Silahkan donlot dari situs resminya, biar aman dari virus, sesuaikan dengan sistem operasi yang anda miliki.

Ada yang versi installer, ada yang portable, untuk lebih lengkap saya coba versi intaller saja (sekitar ratusan Mb).

Seperti biasa, khusus pemula klik saja next terus dan pilih yang default. Tunggu sampai proses instalasi selesai. Lisensinya berbasis GNU, apa itu GNU? Sebenarnya GNU itu kalo dibalik UNG dan kalo dibaca mirip UNIX kan? Sebenarnya UNIX itu rencananya open source, tetapi ditelikung sama vendor jadi berbayar, akhirnya rombongan penggemar open source “beraksi” dengan mengembangkan sejenis UNIX dengan nama UNG yang open source, hingga terciptalah Linux .. katanya. Eh selesai .. instalnya.

Coba dijalankan saja. Test dengan fungsi-fungsi dasarnya, apakah sama dengan matlab? Ternyata tampilan prosesnya agak jadul juga (muncul console window beberapa detik). Tampilannya, mirip-mirip juga sih dengan Scilab dan Matlab.

Ok, fungsi matrix dasar berfungsi dan sama dengan Scilab. Bagaimana dengan programmingnya? Pertanyaan yang sama dengan pembahasan Scilab diawal tulisan. Buka/Open direktori kerja .. kok agak lama ya prosesnya. Sebelumnya saya membuat program dengan bahasa Matlab sebagai berikut:

function y=latih(x)

y=x*2

end

Disimpan dengan nama “latih.m”, oke kita coba jalankan dengan Octave.

>> latih(3)

y = 6

ans = 6

Wow .. dapat dijalankan. Sepertinya octave lebih menarik dari Scilab. Bagaimana untuk program lainnya? Kita coba saja fungsi M-file yang ada di matlab, misalnya fungsi norm yang menghitung normal euclidean (jarak) antara satu object dengan lainnya. Yah .. ternyata fungsi norm ada juga di octave.

Ok, berhubung ada yang bertanya mengenai Fuzzy C-Means (FCM) akan kita coba menjalankan fungsi FCM Matlab di octave .. Hmmm mudah-mudahan berhasil. Mula-Mula kita harus latihan dulu membaca listing code matlab. Fungsi fcm di matlab kelihatannya sederhana tetapi dia memanggil banyak sekali fungsi-fungsi yaitu:

Copy saja seluruh file itu di direktori kerja Anda. Sebenarnya ketika kita menjalankan fungsi fcm di octave, dia akan memberikan pesan error di line tertentu, telusuri saja maka Anda akan menemukan fungsi lainnya yaitu distfcm, initfcm, dst. Ok .. jalankan sesuai instruksi pada help fcm.

data = rand(100,2);
[center,U,obj_fcn] = fcm(data,2);

Ketemu dah pusat clusternya:

>> center
center =
0.59526 0.66670
0.35972 0.27357

Mantap .. FCM dapat berjalan di octave .. Bagaimana dengan Jaringan Syaraf Tiruan? Fuzzy? Coba saja, ga dilarang kok .. Selamat mencoba dan menikmati software Octave yang open source dan gratis dengan bahasa Matlab.